'Tis the season for anecdotes...
I didn't ever take Santa very seriously when I was younger. Or at least, not as far as I can recall. And I thought that no one else took Santa seriously either.
I mean, kids believing in Santa, that's just something that happens in the movies, right? There are countless movies depicting little kids who believe in Santa Claus. They'll write letters to Santa. They'll wait excitedly at the stairs for Santa to come, deliver presents, and eat the cookies and milk. Kids believe in all these elaborate legends and rituals, sometimes even in the face of disbelief from their parents or older kids.
Of course, in these movies, Santa also happens to be real. But Santa isn't real. So why should belief in Santa be real? For me, belief in Santa was all part of the mythos, along with the elves, reindeer, and red suit.
But some time ago, my dad told me that he and my mother made a conscious decision not to emphasize Santa Claus. (They also made a decision not to emphasize heaven and hell, but that's another story.) The reason? Apparently, one of my uncles had a very negative experience with Santa. One year, he found out Santa wasn't real, and he broke down crying. He had a huge tantrum, and IIRC, also questioned the existence of God.
And then the next year, he forgot that Santa wasn't real. And then he found out again and had another tantrum.
So it turns out that my childhood experience was not identical to other people's childhood experiences. And plenty of kids really do believe in Santa, as well as the Tooth Fairy. In a study I found, about 70% of 3-year-olds believe in Santa, as opposed to 78% who believe in the garbage man. 83% of 5-year-olds believe in Santa, and a third of 9-year-olds believe in Santa.
This just boggles my mind. Next you'll tell me that kids actually write letters to Santa (what does the post office even do with them?), actually leave out cookies and milk on Christmas Eve (don't they go bad?), and parents actually dress up as Santa to fool their children. This entails a much greater societal investment into the legend than I previously thought.
And what a bizarre legend it is. Often, it's about the conflict between the believing children and disbelieving adults. And as the narrative goes, it's the children who are in the right for believing. Why?? Why is belief for its own sake a value? It's one thing to claim that it has some value for child psychological development, but I hardly think that the legend has caught the public imagination because of psychological research.
I used to believe we lived in a world where children only believed in Santa in the stories. That world made much more sense, but now I know that is not the world we live in. I guess I learned a valuable lesson in critical thinking.
Wednesday, December 21, 2011
Monday, December 19, 2011
Interlude: God is infinite
This is a continuation of "A few things wrong about the cosmological argument," an ongoing series. This will be a lighter post.
In William Lane Craig's formulation of the Kalam Cosmological argument, he argues that infinities cannot exist, therefore the universe began, therefore God exists.
But... surely God is infinite? You know... actually infinite.
This seems like such a jarring inconsistency in the argument. I give William Lane Craig more credit than that, and I'm sure he has a functional response somewhere. Let's just pretend that I've put in the effort to find his response, and that I've been suitably convinced that of all the problems with the cosmological argument, this is not one of them. *wink*
As many of you know I went to a Catholic high school. It wasn't so bad. Actually a really good high school, run by Jesuits. But yes, it was a religious education. Morning prayers. Religiously infused mission statement. Monthly services. Retreats. A few teachers who were Jesuits. I was Catholic at the time, so I didn't mind. Except for the monthly services. Mass is boring!
I also took some religious classes, learning about the Bible, social justice, and apologetics. They didn't call it apologetics, but that's what it was. The teacher for that class was pretty good. He had a flair for the dramatic and comedic. He used lots of creative teaching techniques, and frequently showed videos. From a high schooler's perspective, showing videos in class was like the best thing ever.
I think he was a fan of William Lane Craig. When I later encountered Lane Craig's arguments, they seemed utterly familiar to me. I consider them to be classic apologetic arguments, though this is perhaps only my perception. "Classic" is just whatever I learned about in high school.
Along the same lines, I also believe that one of the "classic" understandings of God is The Infinite. God isn't merely infinite, God is The Infinite. You can't possibly comprehend God with your finite mind! That would be like trying to comprehend the integers, or quantum field theory! (Silly physicists...)
I took all this stuff with just a grain of salt, but he said one thing that really bothered me. Paraphrased from memory fragments:
This series on the cosmological argument is in about the same spirit. I don't particularly care if people argue for the existence of God. I definitely don't care if people argue about whether God is single or multiple. At least, I don't care in the abstract. But sometimes I see these arguments, and wow! Bad math, bad physics, bad argumental form. If someone argues that we're justified in believing an invisible conscious being that can only touch us in our "hearts", that's okay on some level. (Well, no, it's ridiculous.) But when you start talking bad math? Blasphemy!
A few people have accused me of hiding behind lots of complicated logic, math, and physics. It's all an attempt to dazzle people in to agreeing with me. But that's not the point. The point is to trick you all into reading about logic, math, and physics, when you just wanted a refutation of the cosmological argument. Ha! Ha ha ha!
...
Tune in next time for more of...
"A few things wrong about the cosmological argument"
1. Actual and potential infinities
2. Actual infinities in physics
3. What is real?
4. The "absurdity" of Hilbert's Hotel
5. Interlude: God is infinite
6. Forming Infinity, one by one
7. Uncertain beginnings
8. Entropy: The unsolved problem
9. Kalam as an inductive argument
10. Getting from First Cause to God
In William Lane Craig's formulation of the Kalam Cosmological argument, he argues that infinities cannot exist, therefore the universe began, therefore God exists.
But... surely God is infinite? You know... actually infinite.
This seems like such a jarring inconsistency in the argument. I give William Lane Craig more credit than that, and I'm sure he has a functional response somewhere. Let's just pretend that I've put in the effort to find his response, and that I've been suitably convinced that of all the problems with the cosmological argument, this is not one of them. *wink*
As many of you know I went to a Catholic high school. It wasn't so bad. Actually a really good high school, run by Jesuits. But yes, it was a religious education. Morning prayers. Religiously infused mission statement. Monthly services. Retreats. A few teachers who were Jesuits. I was Catholic at the time, so I didn't mind. Except for the monthly services. Mass is boring!
I also took some religious classes, learning about the Bible, social justice, and apologetics. They didn't call it apologetics, but that's what it was. The teacher for that class was pretty good. He had a flair for the dramatic and comedic. He used lots of creative teaching techniques, and frequently showed videos. From a high schooler's perspective, showing videos in class was like the best thing ever.
I think he was a fan of William Lane Craig. When I later encountered Lane Craig's arguments, they seemed utterly familiar to me. I consider them to be classic apologetic arguments, though this is perhaps only my perception. "Classic" is just whatever I learned about in high school.
Along the same lines, I also believe that one of the "classic" understandings of God is The Infinite. God isn't merely infinite, God is The Infinite. You can't possibly comprehend God with your finite mind! That would be like trying to comprehend the integers, or quantum field theory! (Silly physicists...)
I took all this stuff with just a grain of salt, but he said one thing that really bothered me. Paraphrased from memory fragments:
God is defined as The Infinite. Suppose there were two gods. Then there would be two infinites. But there can only be one infinity, because all infinities are overlapping and identical. Therefore, there can only be one God.Arrrgh! I mean, I don't mind arguing for a single God. Whatever. But man, that is some bad math! The set of even numbers and the set of odd numbers are both infinite but they don't overlap! Also, neither odd nor even numbers are identical to God. This got me to thinking along other lines, like what is God's cardinality? Does God's power set have greater cardinality than God?
This series on the cosmological argument is in about the same spirit. I don't particularly care if people argue for the existence of God. I definitely don't care if people argue about whether God is single or multiple. At least, I don't care in the abstract. But sometimes I see these arguments, and wow! Bad math, bad physics, bad argumental form. If someone argues that we're justified in believing an invisible conscious being that can only touch us in our "hearts", that's okay on some level. (Well, no, it's ridiculous.) But when you start talking bad math? Blasphemy!
A few people have accused me of hiding behind lots of complicated logic, math, and physics. It's all an attempt to dazzle people in to agreeing with me. But that's not the point. The point is to trick you all into reading about logic, math, and physics, when you just wanted a refutation of the cosmological argument. Ha! Ha ha ha!
...
Tune in next time for more of...
"A few things wrong about the cosmological argument"
1. Actual and potential infinities
2. Actual infinities in physics
3. What is real?
4. The "absurdity" of Hilbert's Hotel
5. Interlude: God is infinite
6. Forming Infinity, one by one
7. Uncertain beginnings
8. Entropy: The unsolved problem
9. Kalam as an inductive argument
10. Getting from First Cause to God
Wednesday, December 14, 2011
The "absurdity" of Hilbert's Hotel
This is a continuation of "A few things wrong about the cosmological argument," an ongoing series. Today we will discuss William Lane Craig's treatment of Hilbert's Hotel. I will assume you are familiar with Hilbert's Infinite Hotel; if not, you can read William Lane Craig, me, or any other source on the internet.
William Lane Craig (WLC) thinks Hilbert's Infinite Hotel is absurd. If Hilbert's Hotel is full, then you can add or remove people and it will still have the same number of guests. Absurd!
Of course, WLC thinks there is a more abstract property of Hilbert's Hotel which is absurd. Specifically, he claims it is absurd that you can add or remove things, and still have the same number of things. I do not think this is absurd. The argument from absurdity relies on my agreement at this point, but I do not agree.
(An aside: WLC makes a technical error here. We do not say that there is the "same number" of things, we say that the two sets of things have the "same cardinality". Neither set has a well-defined "number" of things, since both sets are infinite. There is a reason we use technical terms like "cardinality", and it is to avoid making mistakes by accidentally applying intuition where it does not apply. WLC may have simply wanted to avoid technical jargon...)
WLC cites a couple people who objected, like me, that infinities are not absurd. His basic response is, "It looks pretty absurd to me." "Nuh uh." "Yeah too." We seem to be at an impasse. If you're keeping track, that means WLC lost, since he is the one presenting the argument, and he has failed to convince. But let's stop keeping track, and focus on resolving the impasse.
An anecdote: I first learned about infinite sets in high school. This was back in the day, when the internet was still a novelty to me, and I wasn't smart enough to use a pseudonym. I used to exchange puzzles with people and argue about mathematics. In one of these arguments, someone told me to read about infinite set theory. It was crazy! Infinite sets blew my mind. But by the time I got to college, they became intuitive and familiar, like a favorite old joke. Non-math people think that when math people get together, they make jokes about pi and squares. In my experience, they make jokes about infinite sets. And yet, the set of untold jokes about infinite sets remains as big as ever.
I contend that infinities are not "absurd" in the sense of "obviously false". Rather, infinities are only counter-intuitive (and only at first). Infinite set theory is well-established in mathematics. Due to some complications*, it is impossible for me to simply prove that set theory is consistent. But we think that set theory is consistent for the same reason we think arithmetic is consistent, and I don't see WLC waving his arms incredulously at arithmetic.
*See Godel's second incompleteness theorem.
This is a point that clearly needs a response, so WLC has already responded to it.
There is no way to answer these questions, because "absurdity" is an intuitive idea. Either we think something sounds absurd or it doesn't. Intuition doesn't whisper in our ear, "It is absurd in reality, but not mathematics. Also, 'reality' is a category that includes past events, but not future events, and it excludes inconvenient counterexamples." Anyways, my intuition never says anything like that to me.
Put it this way. If WLC didn't know anything about what mathematicians said, he would have guessed infinite sets were bad math. And then when he finds out that it's good math, what is the appropriate response? WLC's response is to say that infinite sets are still absurd, just not in mathematics. I think the proper response is to revise what we previously thought was absurd.
I must say one last thing, as a physicist. WLC thinks absurdity is a good argument against a physical theory? Even when said absurdity is mathematically consistent? I question his knowledge of modern physics.
"A few things wrong about the cosmological argument"
1. Actual and potential infinities
2. Actual infinities in physics
3. What is real?
4. The "absurdity" of Hilbert's Hotel
5. Interlude: God is infinite
6. Forming Infinity, one by one
7. Uncertain beginnings
8. Entropy: The unsolved problem
9. Kalam as an inductive argument
10. Getting from First Cause to God
William Lane Craig (WLC) thinks Hilbert's Infinite Hotel is absurd. If Hilbert's Hotel is full, then you can add or remove people and it will still have the same number of guests. Absurd!
Can anyone sincerely believe that such a hotel could exist in reality? These sorts of absurdities illustrate the impossibility of the existence of an actually infinite number of things.This is an argument from absurdity, which has the following form:
A implies B.There is nothing wrong with an argument from absurdity if it is done correctly. But it is not done correctly. I can agree that Hilbert's Hotel is absurd. But not all infinities are necessarily absurd. We can have infinities without specifically having an infinite hotel. Hilbert's Hotel is absurd because we will never have the resources, the manpower to create such a hotel. We don't have the people to fill it, the means to maintain it.
Both me and my opponents agree that B is obviously false.
Therefore we should agree that A is false.
Of course, WLC thinks there is a more abstract property of Hilbert's Hotel which is absurd. Specifically, he claims it is absurd that you can add or remove things, and still have the same number of things. I do not think this is absurd. The argument from absurdity relies on my agreement at this point, but I do not agree.
(An aside: WLC makes a technical error here. We do not say that there is the "same number" of things, we say that the two sets of things have the "same cardinality". Neither set has a well-defined "number" of things, since both sets are infinite. There is a reason we use technical terms like "cardinality", and it is to avoid making mistakes by accidentally applying intuition where it does not apply. WLC may have simply wanted to avoid technical jargon...)
WLC cites a couple people who objected, like me, that infinities are not absurd. His basic response is, "It looks pretty absurd to me." "Nuh uh." "Yeah too." We seem to be at an impasse. If you're keeping track, that means WLC lost, since he is the one presenting the argument, and he has failed to convince. But let's stop keeping track, and focus on resolving the impasse.
An anecdote: I first learned about infinite sets in high school. This was back in the day, when the internet was still a novelty to me, and I wasn't smart enough to use a pseudonym. I used to exchange puzzles with people and argue about mathematics. In one of these arguments, someone told me to read about infinite set theory. It was crazy! Infinite sets blew my mind. But by the time I got to college, they became intuitive and familiar, like a favorite old joke. Non-math people think that when math people get together, they make jokes about pi and squares. In my experience, they make jokes about infinite sets. And yet, the set of untold jokes about infinite sets remains as big as ever.
I contend that infinities are not "absurd" in the sense of "obviously false". Rather, infinities are only counter-intuitive (and only at first). Infinite set theory is well-established in mathematics. Due to some complications*, it is impossible for me to simply prove that set theory is consistent. But we think that set theory is consistent for the same reason we think arithmetic is consistent, and I don't see WLC waving his arms incredulously at arithmetic.
*See Godel's second incompleteness theorem.
This is a point that clearly needs a response, so WLC has already responded to it.
Hence, one could grant that in the conceptual realm of mathematics one can, given certain conventions and axioms, speak consistently about infinite sets of numbers, but this in no way implies that an actually infinite number of things is really possible.WLC distinguishes between "logical" possibility and "real or factual" possibility. Unfortunately, this places infinite sets in a very odd place. What kind of absurdity is this, that is too absurd for the real world, but not absurd enough for mathematics? And for what kind of "real" is it too absurd for? Lastly, if there are different degrees of absurdity, how do we know which degree it is?
There is no way to answer these questions, because "absurdity" is an intuitive idea. Either we think something sounds absurd or it doesn't. Intuition doesn't whisper in our ear, "It is absurd in reality, but not mathematics. Also, 'reality' is a category that includes past events, but not future events, and it excludes inconvenient counterexamples." Anyways, my intuition never says anything like that to me.
Put it this way. If WLC didn't know anything about what mathematicians said, he would have guessed infinite sets were bad math. And then when he finds out that it's good math, what is the appropriate response? WLC's response is to say that infinite sets are still absurd, just not in mathematics. I think the proper response is to revise what we previously thought was absurd.
I must say one last thing, as a physicist. WLC thinks absurdity is a good argument against a physical theory? Even when said absurdity is mathematically consistent? I question his knowledge of modern physics.
"A few things wrong about the cosmological argument"
1. Actual and potential infinities
2. Actual infinities in physics
3. What is real?
4. The "absurdity" of Hilbert's Hotel
5. Interlude: God is infinite
6. Forming Infinity, one by one
7. Uncertain beginnings
8. Entropy: The unsolved problem
9. Kalam as an inductive argument
10. Getting from First Cause to God
Monday, December 12, 2011
Electrons, gaps, and pseudogaps
I want to give you a bit of flavor of what I've been researching this semester. Problem 1: It is confidential information (there are scientific competitors). Problem 2: It is incomprehensible.
So I'm not going to talk about my research. I'm going to talk about a few of the broad ideas in cutting edge research into high temperature superconductors. The point is not really to teach you about high temperature superconductors (which is hardly useful information if you're not studying superconductors), but so you get the idea of what it looks like.
So. Superconductors. Below a certain temperature "Tc", superconductors conduct electricity perfectly, with no resistance. This property has obvious practical value, but unfortunately all known superconductors have a very low Tc. Even the so-called "high Tc superconductors" discovered in 1986 still have a Tc of about -140 Celsius.
We understand how low Tc superconductors work. The problem was solved in 1957, and the solution is called BCS theory. BCS theory provides a way for electrons to attract each other (despite being opposite charge), and the electron pairs form a Bose-Einstein condensate. The condensate of electron pairs is what makes a superconductor. High Tc superconductors also have condensed electron pairs, but BCS theory doesn't work, and no one knows why the electrons attract each other.
There are two major classes of high Tc superconductors, the cuprates and the iron-based superconductors.* Iron-based superconductors are currently a hot topic because they were just discovered in 2008. But I study cuprates. In particular, I spend most of my time on a material called Bi-2212, which is one of the most highly studied superconductors. I am not sure why it gets so much study, but I would guess that it is because it is cheap, easy to study, and (somewhat self-referentially) has been studied enough that it allows for an ever higher tower of knowledge.
*There are other high Tc superconductors, but I will not speak of them.
I study Bi-2212 using a technique called ARPES. In concept, ARPES is simple: shine light on the material, and look at the ejected electrons. In particular, we look at the direction that the ejected electrons go, and the energy. If we graph the energy of the electrons (vertical axis) vs the angle (horizontal axes), we get something like this:
So I'm not going to talk about my research. I'm going to talk about a few of the broad ideas in cutting edge research into high temperature superconductors. The point is not really to teach you about high temperature superconductors (which is hardly useful information if you're not studying superconductors), but so you get the idea of what it looks like.
So. Superconductors. Below a certain temperature "Tc", superconductors conduct electricity perfectly, with no resistance. This property has obvious practical value, but unfortunately all known superconductors have a very low Tc. Even the so-called "high Tc superconductors" discovered in 1986 still have a Tc of about -140 Celsius.
We understand how low Tc superconductors work. The problem was solved in 1957, and the solution is called BCS theory. BCS theory provides a way for electrons to attract each other (despite being opposite charge), and the electron pairs form a Bose-Einstein condensate. The condensate of electron pairs is what makes a superconductor. High Tc superconductors also have condensed electron pairs, but BCS theory doesn't work, and no one knows why the electrons attract each other.
There are two major classes of high Tc superconductors, the cuprates and the iron-based superconductors.* Iron-based superconductors are currently a hot topic because they were just discovered in 2008. But I study cuprates. In particular, I spend most of my time on a material called Bi-2212, which is one of the most highly studied superconductors. I am not sure why it gets so much study, but I would guess that it is because it is cheap, easy to study, and (somewhat self-referentially) has been studied enough that it allows for an ever higher tower of knowledge.
*There are other high Tc superconductors, but I will not speak of them.
I study Bi-2212 using a technique called ARPES. In concept, ARPES is simple: shine light on the material, and look at the ejected electrons. In particular, we look at the direction that the ejected electrons go, and the energy. If we graph the energy of the electrons (vertical axis) vs the angle (horizontal axes), we get something like this:
From Ronning et al, Science 1998. Figure cropped for clarity. I marked the Fermi Surface in blue. Don't worry about what a quasiparticle is.
Experimental physics being what it is, we don't really see that whole picture there. We see tiny slices of it at a time. If I showed you some real data, it would be unrecognizable.
The way the electrons work, there are a bunch of quantum states for them to fill. The quantum states act like slots, and only one electron fits in each slot. The electrons only fill slots up to a certain energy, but there are more empty slots above that energy. The most interesting physics happens where the filled slots meet the empty slots, what's called the Fermi Surface. In fact, this is where the electron pairs live.
Long story short, when we look at the Fermi Surface of a superconductor, there is a small energy gap between the filled and empty slots. This gap in energy represents the energy required to pull the attractive electrons pairs apart. The fascinating thing about cuprate superconductors, is that the gap is not the same size everywhere on the Fermi Surface.
Also from Ronning et al. The size of the gap has been greatly exaggerated.
Yes, in fact, there are even points on the Fermi Surface where there is no gap at all! These points are called nodes. It would seem that at these nodes, there is no superconductivity happening. This is very different from conventional superconductors, which have gaps everywhere on the Fermi Surface.
And what about iron-based superconductors? Iron-based superconductors also have gaps everywhere, just like conventional superconductors. But it's not quite the same! We have reason to think that there are nodes in iron-based superconductors, but they cannot be seen directly because they are between Fermi Surfaces, rather than on the Fermi Surfaces. Of course, this is not a settled matter...
When you raise the temperature of a superconductor, the superconductivity disappears, and so does the gap. But the cuprates do something funny. The gap remains even at high temperatures, when the material is not a superconductor. Or at least, part of the gap does.
From Lee et al, Nature 2007. Figure cropped for clarity. The horizontal axis is the position in the Fermi Surface; the vertical axis is the size of the gap. The blue and green lines are at superconducting temperatures; the red line is above superconducting temperature.
The gap that remains when the material is no longer superconducting is called the "pseudogap". It's a silly name, since the gap is real. But is the gap there because of incipient superconductivity? Or is it an unrelated property of the material?
Check out the date of that paper. 2007. Scientists are still arguing over the pseudogap. I've seen several talks about it, talks which disagree with each other.
So, that's what superconductivity research looks like. Or at least, that's one very small part of it.
Categories:
condensed matter,
physics,
research
Wednesday, December 7, 2011
Same-sex PDA: reactions
My boyfriend and I are sorta into PDA. What can I say, I like hugging and kissing and holding hands, and I don't mind doing it in public. I think he likes showing me off too.
As you would expect, PDA between two men often gets weird reactions. This is true even in San Francisco. I started collecting a few of these reactions, but I stopped after the novelty wore off. Here they are.
As you would expect, PDA between two men often gets weird reactions. This is true even in San Francisco. I started collecting a few of these reactions, but I stopped after the novelty wore off. Here they are.
Woman on train: How old are you?That one offended my boyfriend.
Me: I'm 22.
Woman: You look 16. I was going to tell you that you shouldn't hold your son that way.
Woman leaves train.
Man on street: Let go.I thought this guy was especially weird because he was walking half a block in front of us, and trying to talk to us.
Man: Let go.
Man: Let go.
Some minutes pass as he repeats himself.
Man: Stop doing that. Come on!
etc.
Female reveler at street fair: Oh, they're so cute!It's funny that she treated us as a novelty, but I guess if we didn't secretly enjoy this sort of thing, we wouldn't be doing PDA.
She hugs us as her friend takes a picture.
We're locked out of my BF's apartment, waiting for the landlady.This guy helped me appreciate how awkward women feel when being propositioned in elevators.
Man walks up to us: Father, son?
BF: No.
Me: *ignore*
Man pesters us for a while, talking nonsense. I get the impression that he's trying to proposition us, but it's unclear. My BF thought he was trying to sell us drugs.
Man: You're not open-minded enough to try black. (The man is black.) Look, he's open-minded enough. (He gestures at me.)
Me: *roll eyes*
Eventually he leaves and the landlady arrives.
Guy on the bus, just as he exits: Faggots... Out in public.I wanna look at this ironically and laugh about it, but having the real experience is just disturbing.
Tuesday, December 6, 2011
Relativism and the gelato guy
Remember the Gelato guy? A few weeks ago at Skepticon 4, the owner of a gelateria posted a sign that said, "Skepticon is NOT welcomed to my Christian Business”. The owner took it down fairly quickly, and posted an apology. In most of the atheist blogs that I pay attention to, people responded very positively to the apology.
I basically don't care about Gelato guy, and I forget which state he's in. But I point this out as a recent example of judging people based on their context, as I discussed in my previous post on cultural relativism.
On an objective measure, I don't think Gelato guy's actions are "positive". I would prefer that businesses don't discriminate in the first place, rather than discriminating and then apologizing for it afterwards.
On the other hand, we intuitively judge people based on what they can be reasonably expected to do. We feel the need to give a person an "out". If we simply condemn people no matter what they do, our condemnations will fail to encourage better behavior. Gelato guy is just going to throw up his hands, because there is no way he can earn PZ's forgiveness.
On the other other hand, who is the audience for our condemnation? Is it the Gelato guy, or is it blog-reading atheists? If the audience is blog-reading atheists, condemnation is useful after all, because atheists can be expected to behave better. As I understand it, this is PZ Myers' goal, to make a statement to atheists, not to Gelato guy. His statement is that atheists should have higher standards, and I sympathize a lot with this message.
On the other other hand, I basically don't care about Gelato guy.
That’s exactly the type of response we want from people who may not agree with us. I don’t know what more we could ask from a Christian. I forgive him. Hell, next time I’m in Springfield, I might even buy some gelato from him.The notable exception was PZ Myers, who made a big deal about rejecting the apology:
--Hemant Mehta
GelatoGuy lives in one of the most religious countries on earth, in a particularly intensely religious part of that country, and in a moment of smug self-righteousness, felt he could openly discriminate against people who do not respect his beliefs. And now he thinks he can walk away, forgiven, and return to his blithe happy Christian pocket universe, just by saying a few words.Someone asked PZ, "Just out of curiosity, what would the guy have to do to be forgiven?" PZ responds, "Nothing. Make an example of him; don't give bigots an out."
I basically don't care about Gelato guy, and I forget which state he's in. But I point this out as a recent example of judging people based on their context, as I discussed in my previous post on cultural relativism.
On an objective measure, I don't think Gelato guy's actions are "positive". I would prefer that businesses don't discriminate in the first place, rather than discriminating and then apologizing for it afterwards.
On the other hand, we intuitively judge people based on what they can be reasonably expected to do. We feel the need to give a person an "out". If we simply condemn people no matter what they do, our condemnations will fail to encourage better behavior. Gelato guy is just going to throw up his hands, because there is no way he can earn PZ's forgiveness.
On the other other hand, who is the audience for our condemnation? Is it the Gelato guy, or is it blog-reading atheists? If the audience is blog-reading atheists, condemnation is useful after all, because atheists can be expected to behave better. As I understand it, this is PZ Myers' goal, to make a statement to atheists, not to Gelato guy. His statement is that atheists should have higher standards, and I sympathize a lot with this message.
On the other other hand, I basically don't care about Gelato guy.
Monday, December 5, 2011
On cultural relativism
Here's a good example of what you might derogatorily call cultural relativism. Coming from Biblical scholars, no less.
In a chapter of The Bible Now, Friedman and Dolansky argue that the Bible's seeming unambiguous condemnations of homosexuality can be ignored, even if you accept the Bible's moral authority. According to a review by Adam Kirsch, this is one of the arguments they make:
As I understand it, cultural relativism is not so much a distinct philosophy, as a term that you use to denigrate philosophies you don't like. But of course, we all know the stereotype of cultural relativism. "Cultures all have different moral guidelines, and we should judge people from the perspective of the culture they come from." Well, what if this culture thinks it is morally correct to apply its own moral guidelines to other cultures, huh?
However, I think there is a grain of wisdom in even the strawiest of cultural relativist strawmen. Allow me illustrate it with faux mathematical graphs.
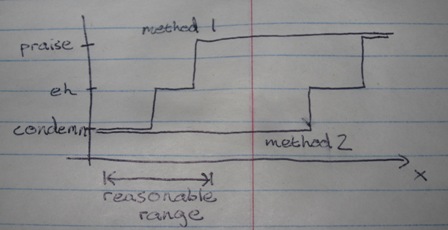
Suppose that there are a variety of actions we can make, and some are morally preferred to others. Let's invent a number "x" which says how strongly a particular action is preferred. A higher value of x corresponds to a greater moral good.
But even though we may prefer x=3 to x=2 to x=1 to x=0, it is hard to express different gradations of moral approval. For the most part, we either express praise, or condemnation, or indifference. So when express judgement, we have to translate this potentially continuous variable x to a discrete value. Here are a few ways to do the translation, though there are many more:
But depending on what culture a person is from, they may have a different range of actions available to them. Either people from that culture believe that a certain range of actions is "reasonable", or the culture punishes people who go outside that range. For example, the authors of the Leviticus could have chosen to express more or less condemnation of homosexuality, but it would be extremely unlikely for them to express anything approaching an enlightened view.
In other words, the authors of Leviticus had various values of x available to them, but all of these available values are very low in my view.
If I were to express praise and condemnation according to method 2, this wouldn't be very effective. No matter what action the ancient people take, I condemn them, so they have no incentive to do better. But if I express praise and condemnation according to method 1, praise is within reach for them! Perhaps this will cause them to change their actions.
And that's why we may want to look at the surrounding culture before issuing judgments about the people in it.
But there's a problem here. The authors of Leviticus aren't listening to my moral praise. They're dead! The only people listening to my moral judgments are people in my culture. Therefore, I'm sticking to method 2. That means universal condemnation of the authors of Leviticus and their surrounding culture.
(via Evolutionblog)
In a chapter of The Bible Now, Friedman and Dolansky argue that the Bible's seeming unambiguous condemnations of homosexuality can be ignored, even if you accept the Bible's moral authority. According to a review by Adam Kirsch, this is one of the arguments they make:
Turning from ancient Israel to Assyria, Egypt, and Greece, Friedman and Dolansky observe that these other Near Eastern societies generally had nothing against homosexual acts as such. They reserved their odium for the passive partner in anal sex, the man who was penetrated.It's not altogether clear to me that killing both men is better than killing just one of them, but let's put that aside. I wish to discuss the question of whether the surrounding culture can make the authors of Leviticus more morally praiseworthy.
...
Why, then, does Leviticus, uniquely among ancient Near Eastern law codes, prescribe death for both partners in homosexual acts? Friedman and Dolansky argue, quoting another Bible scholar, that it is because Leviticus “emphasizes the equality of all. It does not have the class distinctions that are in the other cultures’ laws.”
This is a remarkable performance. Before you know it, a law that unambiguously prescribes death for gay men has been turned into an example of latent egalitarianism.
As I understand it, cultural relativism is not so much a distinct philosophy, as a term that you use to denigrate philosophies you don't like. But of course, we all know the stereotype of cultural relativism. "Cultures all have different moral guidelines, and we should judge people from the perspective of the culture they come from." Well, what if this culture thinks it is morally correct to apply its own moral guidelines to other cultures, huh?
However, I think there is a grain of wisdom in even the strawiest of cultural relativist strawmen. Allow me illustrate it with faux mathematical graphs.
Suppose that there are a variety of actions we can make, and some are morally preferred to others. Let's invent a number "x" which says how strongly a particular action is preferred. A higher value of x corresponds to a greater moral good.
But even though we may prefer x=3 to x=2 to x=1 to x=0, it is hard to express different gradations of moral approval. For the most part, we either express praise, or condemnation, or indifference. So when express judgement, we have to translate this potentially continuous variable x to a discrete value. Here are a few ways to do the translation, though there are many more:
I was too lazy to bust out Mathematica for this one
But depending on what culture a person is from, they may have a different range of actions available to them. Either people from that culture believe that a certain range of actions is "reasonable", or the culture punishes people who go outside that range. For example, the authors of the Leviticus could have chosen to express more or less condemnation of homosexuality, but it would be extremely unlikely for them to express anything approaching an enlightened view.
In other words, the authors of Leviticus had various values of x available to them, but all of these available values are very low in my view.
If I were to express praise and condemnation according to method 2, this wouldn't be very effective. No matter what action the ancient people take, I condemn them, so they have no incentive to do better. But if I express praise and condemnation according to method 1, praise is within reach for them! Perhaps this will cause them to change their actions.
And that's why we may want to look at the surrounding culture before issuing judgments about the people in it.
But there's a problem here. The authors of Leviticus aren't listening to my moral praise. They're dead! The only people listening to my moral judgments are people in my culture. Therefore, I'm sticking to method 2. That means universal condemnation of the authors of Leviticus and their surrounding culture.
(via Evolutionblog)
Categories:
lgbta,
philosophy,
religion
Thursday, December 1, 2011
Science vs Acne
I have pretty bad back acne. No, I will not show you photos. This is not that kind of blog.
I don't really care about my acne. I've shown it scientifically! In the past when I've tried acne medication, my conclusion was that I don't have the motivation to apply the medication on a regular basis, and that medication applied on an irregular basis is ineffective.
But I have new motivation. I have what I'm worried is another abscess. After how painful it was last time, I'm taking someone's suggestion that I apply hot packs to kill the bacteria before it grows big. As long as I'm boiling this water, I might as well kill some acne!
Of course, I'm not actually going to do any science. I am participating in what has been called the "coffeeshop fallacy" (via The Thinker). I like the idea of doing science, but I'm not actually willing to put in the effort. I'm a PhD student, and I have real science to occupy my time! So what I'm actually going to do here is an affectionate parody of science, whatever amuses me.
The hot pack idea comes from Brian Dunning. He cites a study which says you can treat acne by applying 120 farenheit for three minutes twice a day. There's no way I will use such stringent protocols. Brian suggested using a laptop power adapter, but I'm going to use a rag with a bit of boiling water poured on it. I can use the extra boiling water for tea!
The other day I had some Yogi tea called "skin detox". On the label, it said:
I'm taking another idea from XKCD:

On one side of my back, I'll apply the hot pack. On the other side, I may just try some acne medication. Then I will ask my boyfriend to say which side looks better, without telling him which is which. Actually, I will probably use really shoddy blinding, and he'll find out which side is which. But he will appreciate the excuse for me to be topless.
And my excuse for writing about the experiment before it's done is to avoid reporting bias. As you know, scientists are less likely to report negative results than positive ones, which can lead to systematic errors. Therefore, if I never write about this again, you may assume that the results were negative, or that I lost all motivation.
I don't really care about my acne. I've shown it scientifically! In the past when I've tried acne medication, my conclusion was that I don't have the motivation to apply the medication on a regular basis, and that medication applied on an irregular basis is ineffective.
But I have new motivation. I have what I'm worried is another abscess. After how painful it was last time, I'm taking someone's suggestion that I apply hot packs to kill the bacteria before it grows big. As long as I'm boiling this water, I might as well kill some acne!
Of course, I'm not actually going to do any science. I am participating in what has been called the "coffeeshop fallacy" (via The Thinker). I like the idea of doing science, but I'm not actually willing to put in the effort. I'm a PhD student, and I have real science to occupy my time! So what I'm actually going to do here is an affectionate parody of science, whatever amuses me.
The hot pack idea comes from Brian Dunning. He cites a study which says you can treat acne by applying 120 farenheit for three minutes twice a day. There's no way I will use such stringent protocols. Brian suggested using a laptop power adapter, but I'm going to use a rag with a bit of boiling water poured on it. I can use the extra boiling water for tea!
The other day I had some Yogi tea called "skin detox". On the label, it said:
Goodness should become human nature because it is real natureThis so that I can credit the tea later if I get rid of the acne.
I'm taking another idea from XKCD:

On one side of my back, I'll apply the hot pack. On the other side, I may just try some acne medication. Then I will ask my boyfriend to say which side looks better, without telling him which is which. Actually, I will probably use really shoddy blinding, and he'll find out which side is which. But he will appreciate the excuse for me to be topless.
And my excuse for writing about the experiment before it's done is to avoid reporting bias. As you know, scientists are less likely to report negative results than positive ones, which can lead to systematic errors. Therefore, if I never write about this again, you may assume that the results were negative, or that I lost all motivation.
Categories:
comics,
experiments,
real life,
science,
silliness
Wednesday, November 30, 2011
Harry Potter meets rationality
I'm still reading Gravity's Rainbow, which is taking forever. It doesn't help that somewhere in the middle, I decided to take a break, and then the library lost the copy I returned! During my break, I took up a variety of much lighter reading, including Harry Potter and the Methods of Rationality.
This well-known fanfiction takes place in an alternate Potter universe where Harry Potter has been brought up by a scientist. When Harry Potter first discovers the world of magic, he does what any reasonable eleven-year-old would do, and applies the scientific method to it. Harry Potter first tests the existence of magic using pre-agreed protocols. He immediately sees that the wizarding economy is inefficient, and plans to exploit it later. He gets Draco to apply the scientific method to his belief that muggle blood is diluting magic. He tries to use the time-turner to solve NP problems.
Exciting right? I thought it was hilarious. It's also great because it doesn't have as much straw vulcan in it as you might expect. The ideas are mostly taken from the website Less Wrong. Harry Potter isn't right all the time, but that's because he is prey to cognitive bias like anyone else, not because he is "too rational".
But it's not merely about delivering lessons about rationality. Nor is it just about parodying the sillier things the Harry Potter universe. It starts out that way, but soon develops its own story, distinct from the original Harry Potter. It has its share of mysteries, dramas, and dynamic characters. The story discusses many themes that even rational people may disagree on. For example, Professor Quirrell's character has been replaced by a very different character, one who becomes Harry Potter's morally ambiguous mentor.
But since I'm giving this a review, I must also express a few complaints. Though I loved many of the things in the later chapters (eg Hermione calls out Dumbledore for his clear bias towards male heroes), I sort of liked the earlier chapters which were funnier and less serious. I felt the "Humanism" chapters were obnoxious. Harry Potter finds some sappy secular-humanistic way to deal with Dementors. This is pretentious and cliched, and my tastes are too ironic for that sort of thing.
Also, it is much longer than it needs to be. It's not even complete yet, and it's over a thousand pages. I felt way too much time was spent on these wizarding battles that Quirrell uses to teach the kids how to fight. It's a lot like Ender's Game where it goes in great depth about the weightless battles in Ender's military school. I don't particularly care for Ender's Game, or for that part of the book. Quidditch may be an objectively terrible game, but at least it only took up a small part of the books!
But on the whole I enjoyed the work, and I would continue reading it once it gets updated. I highly recommend reading the first few chapters, which are fun even if you don't want to really get into it.
This well-known fanfiction takes place in an alternate Potter universe where Harry Potter has been brought up by a scientist. When Harry Potter first discovers the world of magic, he does what any reasonable eleven-year-old would do, and applies the scientific method to it. Harry Potter first tests the existence of magic using pre-agreed protocols. He immediately sees that the wizarding economy is inefficient, and plans to exploit it later. He gets Draco to apply the scientific method to his belief that muggle blood is diluting magic. He tries to use the time-turner to solve NP problems.
Exciting right? I thought it was hilarious. It's also great because it doesn't have as much straw vulcan in it as you might expect. The ideas are mostly taken from the website Less Wrong. Harry Potter isn't right all the time, but that's because he is prey to cognitive bias like anyone else, not because he is "too rational".
But it's not merely about delivering lessons about rationality. Nor is it just about parodying the sillier things the Harry Potter universe. It starts out that way, but soon develops its own story, distinct from the original Harry Potter. It has its share of mysteries, dramas, and dynamic characters. The story discusses many themes that even rational people may disagree on. For example, Professor Quirrell's character has been replaced by a very different character, one who becomes Harry Potter's morally ambiguous mentor.
But since I'm giving this a review, I must also express a few complaints. Though I loved many of the things in the later chapters (eg Hermione calls out Dumbledore for his clear bias towards male heroes), I sort of liked the earlier chapters which were funnier and less serious. I felt the "Humanism" chapters were obnoxious. Harry Potter finds some sappy secular-humanistic way to deal with Dementors. This is pretentious and cliched, and my tastes are too ironic for that sort of thing.
Also, it is much longer than it needs to be. It's not even complete yet, and it's over a thousand pages. I felt way too much time was spent on these wizarding battles that Quirrell uses to teach the kids how to fight. It's a lot like Ender's Game where it goes in great depth about the weightless battles in Ender's military school. I don't particularly care for Ender's Game, or for that part of the book. Quidditch may be an objectively terrible game, but at least it only took up a small part of the books!
But on the whole I enjoyed the work, and I would continue reading it once it gets updated. I highly recommend reading the first few chapters, which are fun even if you don't want to really get into it.
Tuesday, November 22, 2011
Fillomino #2
A few months ago, I submitted a fillomino (aka polyominous) puzzle to a puzzle design competition on A Cleverly Titled Logic Puzzle Blog. I think this is the second one I've ever designed (here's the first).
Rules of fillomino:
1. Divide the grid into polyominoes, which are connected shapes made from the little squares. For example, tetris pieces are polyominoes made of four squares.
2. Fill each square with a number, representing the number of little squares in that polyomino.
3. No two polyominoes with the same numbers may share an edge.
4. Some of the numbers are given, but some polyominoes may be implied and have no given numbers.
Solvers voted on the puzzles they liked best. Mine got second, which might reflect on the kind of people who voted. Seriously, they clearly had a taste for rather difficult puzzles.
You may email solutions to skepticsplay at gmail dot com. Enjoy your Thanksgiving!
Rules of fillomino:
1. Divide the grid into polyominoes, which are connected shapes made from the little squares. For example, tetris pieces are polyominoes made of four squares.
2. Fill each square with a number, representing the number of little squares in that polyomino.
3. No two polyominoes with the same numbers may share an edge.
4. Some of the numbers are given, but some polyominoes may be implied and have no given numbers.
Solvers voted on the puzzles they liked best. Mine got second, which might reflect on the kind of people who voted. Seriously, they clearly had a taste for rather difficult puzzles.
You may email solutions to skepticsplay at gmail dot com. Enjoy your Thanksgiving!
Saturday, November 19, 2011
New theorem: Quantum states are real
There's a new paper on arxiv called "The quantum state cannot be interpreted statistically". It has a theorem which proves that, given a few basic assumptions, the quantum state (ie the wavefunction) must be real, rather than a merely statistical object. Nature has an article which mostly just harps on how "seismic" the paper is.
Nature (correction: the article's author, not Nature itself) compares its importance to Bell's Theorem, which is a very important result indeed from 1964. Bell's theorem proved that if there were "hidden variables" underneath the quantum state, then entangled particles must be communicating with each other faster than light. I've explained Bell's theorem in the past.
I felt the news coverage left a lot of unanswered questions. What do they even mean by the "statistical interpretation" of quantum mechanics? Roughly how is it proven? What is the difference between this and Bell's theorem? I found the answers in the arxiv print, and will attempt to summarize them.
What does the "statistical interpretation" mean?
Let's say that we have two ways of flipping a coin. The first method leads to a 50% chance of heads, and a 50% chance of tails. The second method rigs it so the coin always comes up heads. Let's say that I flipped a coin by one of these two methods, and showed you the result. If the coin was heads, then you would not know which method I used.
Now say that I have two ways of preparing an electron. And suppose that you measured the vertical spin component of the electron. If I use the first method, there is a 50% chance the electron is spin up, and 50% chance spin down. If I use the second method, the electron will always be spin up. If I prepared the electron by one of these two methods, and you found that the electron is spin up, you would not know which method I used.
But electron spin is a little trickier than coin flips, because you can measure the spin component in any direction. Suppose you had tried to measure the horizontal spin component, would you always be able to tell which method I used then? The answer is no. But perhaps there is yet another way to measure it?
The authors equate the "statistical interpretation" with the following: Given any two distinct ways to prepare a quantum state, there is a nonzero probability that the result is consistent with either method of preparation. In other words, no matter what kind of measurement we make, there is a chance that we'll get an outcome that doesn't tell us anything.
What's the difference between this theorem and Bell's Theorem?
Bell's theorem requires that you take many measurements and compile statistics of these measurements. Once you are confident enough in your statistics, you can show that the probabilities are incompatible with the "hidden variable" view of quantum mechanics.
This new theorem requires only one measurement. One measurement, and you're done. (Of course, if you have a noisy experiment, you may need to repeat it to build confidence in your result.)
Of course, the new theorem and Bell's theorem also have a slightly different set of assumptions, and slightly different conclusions. But I think the primary difference is that the new theorem requires one measurement, while Bell's theorem requires compiling statistics.
Roughly how is it proven?
As an example, let's take the two methods of preparing an electron that I described above. It turns out that no matter what measurement I make, there is a chance of an outcome that is consistent with either method A or method B.
But we can be tricky. Let's duplicate the machine that prepares the electrons, and assume that these machines are independent of each other. Now there are four methods of preparation:
But it turns out that there is a measurement we can make with four possible outcomes. And each outcome is inconsistent with one of the methods.
The same theorem can be generalized to any two methods of preparing a quantum state. Suppose that one method always produces a spin up electron, and the other produces a spin up electron 99% of the time. All you have to do is have N duplicates of the electron-producing machine (in this case, N=15 suffices), and take a special measurement. No matter the outcome of this measurement is, it is inconsistent with one of the 2^N possible methods of preparation.
The conclusion is that any two distinct quantum states are not just "probably" different, but always different. You just need a tricky measurement to show it.
Is this paper as groundbreaking as Nature claims?
I don't know.
Nature (correction: the article's author, not Nature itself) compares its importance to Bell's Theorem, which is a very important result indeed from 1964. Bell's theorem proved that if there were "hidden variables" underneath the quantum state, then entangled particles must be communicating with each other faster than light. I've explained Bell's theorem in the past.
I felt the news coverage left a lot of unanswered questions. What do they even mean by the "statistical interpretation" of quantum mechanics? Roughly how is it proven? What is the difference between this and Bell's theorem? I found the answers in the arxiv print, and will attempt to summarize them.
What does the "statistical interpretation" mean?
Let's say that we have two ways of flipping a coin. The first method leads to a 50% chance of heads, and a 50% chance of tails. The second method rigs it so the coin always comes up heads. Let's say that I flipped a coin by one of these two methods, and showed you the result. If the coin was heads, then you would not know which method I used.
Now say that I have two ways of preparing an electron. And suppose that you measured the vertical spin component of the electron. If I use the first method, there is a 50% chance the electron is spin up, and 50% chance spin down. If I use the second method, the electron will always be spin up. If I prepared the electron by one of these two methods, and you found that the electron is spin up, you would not know which method I used.
But electron spin is a little trickier than coin flips, because you can measure the spin component in any direction. Suppose you had tried to measure the horizontal spin component, would you always be able to tell which method I used then? The answer is no. But perhaps there is yet another way to measure it?
The authors equate the "statistical interpretation" with the following: Given any two distinct ways to prepare a quantum state, there is a nonzero probability that the result is consistent with either method of preparation. In other words, no matter what kind of measurement we make, there is a chance that we'll get an outcome that doesn't tell us anything.
What's the difference between this theorem and Bell's Theorem?
Bell's theorem requires that you take many measurements and compile statistics of these measurements. Once you are confident enough in your statistics, you can show that the probabilities are incompatible with the "hidden variable" view of quantum mechanics.
This new theorem requires only one measurement. One measurement, and you're done. (Of course, if you have a noisy experiment, you may need to repeat it to build confidence in your result.)
Of course, the new theorem and Bell's theorem also have a slightly different set of assumptions, and slightly different conclusions. But I think the primary difference is that the new theorem requires one measurement, while Bell's theorem requires compiling statistics.
Roughly how is it proven?
As an example, let's take the two methods of preparing an electron that I described above. It turns out that no matter what measurement I make, there is a chance of an outcome that is consistent with either method A or method B.
But we can be tricky. Let's duplicate the machine that prepares the electrons, and assume that these machines are independent of each other. Now there are four methods of preparation:
- A and A (ie both machines use method A)
- A and B
- B and A
- B and B
But it turns out that there is a measurement we can make with four possible outcomes. And each outcome is inconsistent with one of the methods.
- Outcome 1: inconsistent with method 1
- Outcome 2: inconsistent with method 2
- Outcome 3: inconsistent with method 3
- Outcome 4: inconsistent with method 4
The same theorem can be generalized to any two methods of preparing a quantum state. Suppose that one method always produces a spin up electron, and the other produces a spin up electron 99% of the time. All you have to do is have N duplicates of the electron-producing machine (in this case, N=15 suffices), and take a special measurement. No matter the outcome of this measurement is, it is inconsistent with one of the 2^N possible methods of preparation.
The conclusion is that any two distinct quantum states are not just "probably" different, but always different. You just need a tricky measurement to show it.
Is this paper as groundbreaking as Nature claims?
I don't know.
Categories:
news,
physics,
quantum mechanics
Friday, November 18, 2011
Question First vs Answer First
Among the interests represented on my blog, puzzles are the oldest. Writing puzzles used to be a hobby of mine back in high school, when I'd write and submit puzzles to a website. Naturally, the website was full of expert puzzle solvers, so that explains why I am unable to write a puzzle of reasonable difficulty.
In high school, I had a half-baked philosophy of puzzle-writing. There are essentially two ways to write a puzzle: Question First, or Answer First.
In the Answer First method, first you think up a clever idea. And then you try to design a puzzle such that the clever idea is the answer. For example, a folk remedy for hiccups is to scare someone. So there's a classic riddle based on this idea:
In the Question First method, first you think of an interesting problem. And then you check to see if there's an interesting solution to it. For example, a recent puzzle, "Tower of Hanoi Variant" is clearly a Question First puzzle. I was inspired by a problem posed in the game of Freecell; I only tried to find a solution after the fact.
The Answer First method requires quite a bit of creative insight to use, but the Question First method has its own difficulties. When you find an interesting question, there is no guarantee that there is a solution, or that the solution is interesting. And a lot of times, you don't want to just think up one interesting question, you want to think up a whole set of interesting questions. And then you have to look at all of those questions, and see which one has the most interesting answer.
For example, in "Ten Rows of Three", I asked solvers to arrange nine dots into ten rows of three. But I could just as easily ask solvers to arrange X dots into Y rows of Z. What values of X, Y, and Z lead to the most interesting puzzle?
So not only do I need to find a solution without any hints, or even a guarantee that a solution exists, as a puzzle-writer I also have to solve a much larger set of puzzles than the puzzle-solver. This is my secret to being good at puzzle-solving. Write lots of puzzles and then you will become very good at solving them.
But I am not sure that the Question First vs Answer First dichotomy applies to all puzzles (that's why I say the philosophy is half-baked). For example, where does Fillomino fit in? Designing one of these puzzles involves filling more and more clues in, while trying to see what deductions you can make from those clues. But often, the clues we fill in are decided by something that the designer wants in the solution. Depending on the puzzle-designer, it could be more Question First or more Answer First.
My inner skeptic wanted to write a comparison between the Question/Answer First methods of puzzle-writing and the experimental/theoretical methods of science. But my inner skeptic's inner skeptic said that this is ridiculous.
In high school, I had a half-baked philosophy of puzzle-writing. There are essentially two ways to write a puzzle: Question First, or Answer First.
In the Answer First method, first you think up a clever idea. And then you try to design a puzzle such that the clever idea is the answer. For example, a folk remedy for hiccups is to scare someone. So there's a classic riddle based on this idea:
A man walks into a bar and asks for a glass of water. The bartender pulls out a gun, and the man thanks her. What happened?I've also written Answer First puzzles of my own. "Fast Clock, Slow Clock" is an unambiguous example, as is "Guess the Meaning". You can usually recognize Answer First puzzles by their clever "Aha!" solutions. All riddles are Answer First puzzles.
In the Question First method, first you think of an interesting problem. And then you check to see if there's an interesting solution to it. For example, a recent puzzle, "Tower of Hanoi Variant" is clearly a Question First puzzle. I was inspired by a problem posed in the game of Freecell; I only tried to find a solution after the fact.
The Answer First method requires quite a bit of creative insight to use, but the Question First method has its own difficulties. When you find an interesting question, there is no guarantee that there is a solution, or that the solution is interesting. And a lot of times, you don't want to just think up one interesting question, you want to think up a whole set of interesting questions. And then you have to look at all of those questions, and see which one has the most interesting answer.
For example, in "Ten Rows of Three", I asked solvers to arrange nine dots into ten rows of three. But I could just as easily ask solvers to arrange X dots into Y rows of Z. What values of X, Y, and Z lead to the most interesting puzzle?
So not only do I need to find a solution without any hints, or even a guarantee that a solution exists, as a puzzle-writer I also have to solve a much larger set of puzzles than the puzzle-solver. This is my secret to being good at puzzle-solving. Write lots of puzzles and then you will become very good at solving them.
But I am not sure that the Question First vs Answer First dichotomy applies to all puzzles (that's why I say the philosophy is half-baked). For example, where does Fillomino fit in? Designing one of these puzzles involves filling more and more clues in, while trying to see what deductions you can make from those clues. But often, the clues we fill in are decided by something that the designer wants in the solution. Depending on the puzzle-designer, it could be more Question First or more Answer First.
My inner skeptic wanted to write a comparison between the Question/Answer First methods of puzzle-writing and the experimental/theoretical methods of science. But my inner skeptic's inner skeptic said that this is ridiculous.
Wednesday, November 16, 2011
Stats on Catholic dissent
Hemant Mehta posted some statistics on Catholic attitudes and beliefs in America. The one-sentence summary is that Catholics don't really fall in line with official Catholic Church teachings.* For example, only 21% of Catholics believe that having celibate male-only clergy is an important aspect of Catholicism, and 60% say you can be a good Catholic without adhering to church teachings on birth control.
*Not news
What struck me, were the statistics on transubstantiation.
In case you didn't catch it, 50% are aware that the Catholic Church teaches that transubstantiation is real rather than symbolic.1 But a higher percentage, 63%, believe it is real. The 17% "unknowing believers" are Catholics who don't know the Catholic Church's teachings, but believe them anyway.
The source of the statistics, the National Catholic Reporter offers this explanation:
1. From the Catechism of the Catholic Church:
*Not news
What struck me, were the statistics on transubstantiation.
In case you didn't catch it, 50% are aware that the Catholic Church teaches that transubstantiation is real rather than symbolic.1 But a higher percentage, 63%, believe it is real. The 17% "unknowing believers" are Catholics who don't know the Catholic Church's teachings, but believe them anyway.
The source of the statistics, the National Catholic Reporter offers this explanation:
Perhaps this is just a classic case of source amnesia -- people believe many things that they have learned even though they are unable to recall the source of that belief.Somehow, I feel insulted on behalf of reality. It's like, people aren't even believing these things on the basis of some authority, they just believe them on the basis of... well, they forgot.
1. From the Catechism of the Catholic Church:
1374 ... In the most blessed sacrament of the Eucharist "the body and blood, together with the soul and divinity, of our Lord Jesus Christ and, therefore, the whole Christ is truly, really, and substantially contained." "This presence is called 'real' - by which is not intended to exclude the other types of presence as if they could not be 'real' too, but because it is presence in the fullest sense: that is to say, it is a substantial presence by which Christ, God and man, makes himself wholly and entirely present."
1381 "That in this sacrament are the true Body of Christ and his true Blood is something that 'cannot be apprehended by the senses,' says St. Thomas, 'but only by faith, which relies on divine authority.' ...
Monday, November 14, 2011
Attraction is like wine
This essay was written for this month's Carnival of Aces.
I don't drink wine because wine gives me worse Asian glow than any other form of alcohol. But of course I've seen wine. They often have these colorful descriptions on the back. For example...
The asexual community is a bit like a wine tasting community, except that they taste different kinds of attraction. While the dictionary of attraction is not as large as the one for wines, I could come up with a dozen just off the top of my head.* And people still struggle to find words to describe their experiences, often resorting to long stories to do so.
I'm not sure why asexuals are such connoisseurs, but it at least makes sense. Imagine you're in a society that drinks wine, but doesn't care about, and hardly seems to recognize the existence of different kinds of wine. And then you have this group of people who can't stand white wine, but some of them enjoy red wine. Since we know there's at least a distinction between red and white wine, maybe there are distinctions between different types of red wine. Wow, let's go investigate!
And then the red-wine-drinkers tell the rest of society, "Look at all these different flavors of red wine we found. I bet there are lots of flavors of white wine too!" The rest of society shrugs unenthusiastically. Sure, wine is complicated, but do we really need to create so many words to describe it? Wine is wine!
I feel sympathy for both sides, the connoisseurs and the "wine is wine" folks. I don't see why they can't coexist peacefully.
Different flavors of attraction are pretty important to me. Aesthetic attraction and limerence are particularly important to me, because that's what I'm most notably missing. Basically, I don't have a sense of "hotness", or "cuteness", or what have you. And I don't get crushes. Thus it seems obvious to me that we must separate out aesthetic attraction and limerence.
But on the other hand, I can't really tell the difference between sexual and romantic attraction. And I don't really know what platonic attraction is. From the perspective of the asexual community, this is a big blind spot! It's like being unable to distinguish between red and white wine, or not knowing what tannin is.*
*I do not know what tannin is.
Why can't I understand the distinction between romantic and sexual attraction? Maybe I just haven't experienced enough, or I haven't done enough introspection. Maybe I have a genetic insensitivity to a particular flavor. Or maybe the words are poorly defined. Maybe they don't describe single flavors but collections of flavors. Or maybe I'm having trouble connecting the words to their meanings. Nobody can hand me a glass-full and tell me that this is what romantic attraction tastes like. Or maybe everyone else is having the same problem connecting words to meanings, so that the words to really mean different things to different people.
Some people complain to me that asexuals make everything too complicated. All I can do is shrug. Some of those concepts are really important to me, because they hit on a key aspect of my experience. Some words are just meaningless to me, and I only keep track of them as words that are meaningful to other people. Surely, if sexuality is complicated, people are allowed to discuss what exactly is complicated about it for them.
I don't drink wine because wine gives me worse Asian glow than any other form of alcohol. But of course I've seen wine. They often have these colorful descriptions on the back. For example...
A firm, full textured almost focused Cabernet. Spews bing-cherry, unripe apple and lingering tomato.Actually, I took these from a Silly Tasting Note Generator, and I'm sure that if you actually drink wine, they look awfully silly. Not that I can tell. Wikipedia helpfully offers a dictionary of wine tasting descriptors, but I think wine tasting is one of those rare things that you can't learn from the internet.
Wholly obtuse and yellowed Dessert wine. A mouthful of smoked ham, sassy french onion soup and a modicum of Baby Ruth bar.
The asexual community is a bit like a wine tasting community, except that they taste different kinds of attraction. While the dictionary of attraction is not as large as the one for wines, I could come up with a dozen just off the top of my head.* And people still struggle to find words to describe their experiences, often resorting to long stories to do so.
*Ahem. Sexual attraction, romantic attraction, sex drive, sexual fantasies, sexual desire, primary attraction, secondary attraction, aesthetic attraction, sensual attraction, limerence, platonic attraction, platonic crushes, and that's not even half of it.
I'm not sure why asexuals are such connoisseurs, but it at least makes sense. Imagine you're in a society that drinks wine, but doesn't care about, and hardly seems to recognize the existence of different kinds of wine. And then you have this group of people who can't stand white wine, but some of them enjoy red wine. Since we know there's at least a distinction between red and white wine, maybe there are distinctions between different types of red wine. Wow, let's go investigate!
And then the red-wine-drinkers tell the rest of society, "Look at all these different flavors of red wine we found. I bet there are lots of flavors of white wine too!" The rest of society shrugs unenthusiastically. Sure, wine is complicated, but do we really need to create so many words to describe it? Wine is wine!
I feel sympathy for both sides, the connoisseurs and the "wine is wine" folks. I don't see why they can't coexist peacefully.
Different flavors of attraction are pretty important to me. Aesthetic attraction and limerence are particularly important to me, because that's what I'm most notably missing. Basically, I don't have a sense of "hotness", or "cuteness", or what have you. And I don't get crushes. Thus it seems obvious to me that we must separate out aesthetic attraction and limerence.
But on the other hand, I can't really tell the difference between sexual and romantic attraction. And I don't really know what platonic attraction is. From the perspective of the asexual community, this is a big blind spot! It's like being unable to distinguish between red and white wine, or not knowing what tannin is.*
*I do not know what tannin is.
Why can't I understand the distinction between romantic and sexual attraction? Maybe I just haven't experienced enough, or I haven't done enough introspection. Maybe I have a genetic insensitivity to a particular flavor. Or maybe the words are poorly defined. Maybe they don't describe single flavors but collections of flavors. Or maybe I'm having trouble connecting the words to their meanings. Nobody can hand me a glass-full and tell me that this is what romantic attraction tastes like. Or maybe everyone else is having the same problem connecting words to meanings, so that the words to really mean different things to different people.
Some people complain to me that asexuals make everything too complicated. All I can do is shrug. Some of those concepts are really important to me, because they hit on a key aspect of my experience. Some words are just meaningless to me, and I only keep track of them as words that are meaningful to other people. Surely, if sexuality is complicated, people are allowed to discuss what exactly is complicated about it for them.
Thursday, November 10, 2011
Why atheists focus on certain religions
Why do atheists always focus on Christianity? Why not focus on a much more harmful religion, like Islam?
or...
Why do atheists always focus on fundamentalist Christianity? Why not focus on more reasonable forms of religion, like mine?
These are some of those questions people ask vocal atheists (in the US). But to any vocal atheist, a handful of answers are immediately obvious. Here are a few...
The atheist movement prioritizes social change over academic debate. The calm and methodical search for truth is a worthy goal, but one also has to admit the importance of actually getting things done. Religion is not just some academic hypothesis, it's something that actually causes people to kick out their children, oppose LGBT rights, and make poor medical decisions. If that is something we want to change, we do not criticize the most compassionate and reasonable religions, we criticize the least reasonable, most harmful, and most popular religions.
Atheists are focused on here and now. This is not simply due to the desire to create change where it will most benefit ourselves. It is also because we have more power to change the here and now. Islam is pretty bad, but has the most impact far away. Local attitudes are easier to change.
It is likely that you are viewing atheists through a filter. Atheists actually do criticize Islam, liberal Christianity, eastern religions, new age religions, as well as non-religion things like alternative medicine. But the criticism that actually gets widely propagated is the stuff that's most relevant to people, or most exciting. For example, I think atheist criticism of Jainism would be vaguely interesting, but not that interesting, because, honestly, I've never met a Jainist in my life. And I think there is popular appeal in seeing the most extreme atheists and fundamentalist Christians just duke it out. If people want it, then people get it.
Atheists write what they know. That means they'll talk about what's in the news they read. It also means they'll talk about their personal experiences. Even when atheists talk about abstract arguments, they're often inspired by some real argument they had with someone, or an article they read. The same is true about most things people write on any subject.
I'm sure readers can come up with other reasons as well.
My advice to people who think atheists are just focusing on straw men: Relax! If a particular criticism of religious beliefs doesn't apply to your beliefs, then it doesn't apply to your beliefs.
or...
Why do atheists always focus on fundamentalist Christianity? Why not focus on more reasonable forms of religion, like mine?
These are some of those questions people ask vocal atheists (in the US). But to any vocal atheist, a handful of answers are immediately obvious. Here are a few...
The atheist movement prioritizes social change over academic debate. The calm and methodical search for truth is a worthy goal, but one also has to admit the importance of actually getting things done. Religion is not just some academic hypothesis, it's something that actually causes people to kick out their children, oppose LGBT rights, and make poor medical decisions. If that is something we want to change, we do not criticize the most compassionate and reasonable religions, we criticize the least reasonable, most harmful, and most popular religions.
Atheists are focused on here and now. This is not simply due to the desire to create change where it will most benefit ourselves. It is also because we have more power to change the here and now. Islam is pretty bad, but has the most impact far away. Local attitudes are easier to change.
It is likely that you are viewing atheists through a filter. Atheists actually do criticize Islam, liberal Christianity, eastern religions, new age religions, as well as non-religion things like alternative medicine. But the criticism that actually gets widely propagated is the stuff that's most relevant to people, or most exciting. For example, I think atheist criticism of Jainism would be vaguely interesting, but not that interesting, because, honestly, I've never met a Jainist in my life. And I think there is popular appeal in seeing the most extreme atheists and fundamentalist Christians just duke it out. If people want it, then people get it.
Atheists write what they know. That means they'll talk about what's in the news they read. It also means they'll talk about their personal experiences. Even when atheists talk about abstract arguments, they're often inspired by some real argument they had with someone, or an article they read. The same is true about most things people write on any subject.
I'm sure readers can come up with other reasons as well.
My advice to people who think atheists are just focusing on straw men: Relax! If a particular criticism of religious beliefs doesn't apply to your beliefs, then it doesn't apply to your beliefs.
Tuesday, November 8, 2011
Solution to Tower of Hanoi variant
See the original puzzle
Hint: The number of disks you can move increases exponentially as you add more rods.
Still give up?
It's relatively easy to simply show the steps when there are only five rods, but I want to generalize. This requires some recursive algorithms. Advanced puzzle solving ahead!
First, let's define a function G(N), which is the tallest tower we can move if there are N empty rods. In the puzzle, I asked for the tallest tower we can move when there are five rods. Four of those rods are empty, so I basically asked for the value of G(4). I'll give it away right now, G(4) = 15.
But what happens if we have a tower with sixteen disks? We can't simply move the top fifteen disks, and ignore the bottom one. The bottom disk gets in the way, and can't be treated like an empty rod. Therefore, I need to define another function F(N), which is the largest stack of disks we can move from an infinitely tall tower to an empty rod when there are N available empty rods.
Procedure 1: Moving F(N) disks from a big tower to an empty rod, when there are N available empty rods
If N=1, simply move one disk and you're done!
Otherwise...
1. Use Procedure 1 to move F(N-1) disks from the big tower to the first empty rod.
2. Use Procedure 1 to move F(N-2) disks from the big tower to the next empty rod.
3. Continue as above until we get to F(1)
4. Move one disk to the last empty rod.
5. Use Procedure 1 in reverse order to move F(1) disks from the second to last rod onto the last rod.
6. Use Procedure 1 in reverse order to move F(2) disks from the third to last rod onto the last rod.
7. Continue as above until we get to F(N-1).
This procedure allows you to move F(N) = 1 + F(1) + F(2) + ... F(N-1) disks. F(N) is given by this recursive function, but we can also figure out an explicit formula. F(N) = 2^(N-1).
Procedure 2: Moving a tower with G(N) disks to another rod, when there are N available empty rods.
1. Use Procedure 1 to move F(N) disks from the big tower to the first empty rod.
2. Use Procedure 1 to move F(N-1) disks from the big tower to the first empty rod.
3. Continue as above until we get to F(1). By now we should have depleted the big tower of disks.
4. Reverse steps 1 through 3, only now we build the tower on the last rod instead of where it was before.
This procedure allows you to move G(N) = F(1) + F(2) + ... F(N) disks. So G(N) = (2^N) - 1.
G(4) = 15
G(5) = 31
G(6) = 63
etc.
I am sure that this is the best you can do, but I will not provide a proof.
Hint: The number of disks you can move increases exponentially as you add more rods.
Still give up?
It's relatively easy to simply show the steps when there are only five rods, but I want to generalize. This requires some recursive algorithms. Advanced puzzle solving ahead!
First, let's define a function G(N), which is the tallest tower we can move if there are N empty rods. In the puzzle, I asked for the tallest tower we can move when there are five rods. Four of those rods are empty, so I basically asked for the value of G(4). I'll give it away right now, G(4) = 15.
But what happens if we have a tower with sixteen disks? We can't simply move the top fifteen disks, and ignore the bottom one. The bottom disk gets in the way, and can't be treated like an empty rod. Therefore, I need to define another function F(N), which is the largest stack of disks we can move from an infinitely tall tower to an empty rod when there are N available empty rods.
Procedure 1: Moving F(N) disks from a big tower to an empty rod, when there are N available empty rods
If N=1, simply move one disk and you're done!
Otherwise...
1. Use Procedure 1 to move F(N-1) disks from the big tower to the first empty rod.
2. Use Procedure 1 to move F(N-2) disks from the big tower to the next empty rod.
3. Continue as above until we get to F(1)
4. Move one disk to the last empty rod.
5. Use Procedure 1 in reverse order to move F(1) disks from the second to last rod onto the last rod.
6. Use Procedure 1 in reverse order to move F(2) disks from the third to last rod onto the last rod.
7. Continue as above until we get to F(N-1).
This procedure allows you to move F(N) = 1 + F(1) + F(2) + ... F(N-1) disks. F(N) is given by this recursive function, but we can also figure out an explicit formula. F(N) = 2^(N-1).
Procedure 2: Moving a tower with G(N) disks to another rod, when there are N available empty rods.
1. Use Procedure 1 to move F(N) disks from the big tower to the first empty rod.
2. Use Procedure 1 to move F(N-1) disks from the big tower to the first empty rod.
3. Continue as above until we get to F(1). By now we should have depleted the big tower of disks.
4. Reverse steps 1 through 3, only now we build the tower on the last rod instead of where it was before.
This procedure allows you to move G(N) = F(1) + F(2) + ... F(N) disks. So G(N) = (2^N) - 1.
G(4) = 15
G(5) = 31
G(6) = 63
etc.
I am sure that this is the best you can do, but I will not provide a proof.
Friday, November 4, 2011
The size of the observable universe
Previously, I analogized the expansion of the universe to a stretching of a rubber band. Light that travels across the universe is like an ant crawling on that rubber band. Whether the ant ever reaches the other side of the rubber band depends on how fast the rubber band is stretching.
Here, I will introduce something called the scale factor. The scale factor is similar in concept to the total length of the rubber band. The tricky part is that there is no "total length" of the universe, because the universe (as far as we know) is infinitely long. But even if the rubber band were infinitely long, we can still imagine it stretching.
Even without referring to the "ends" of the rubber band, we can still see that the ants are getting further apart. Similarly, even though the universe has no "ends", we can still observe galaxies getting farther apart. There are some complications (like if the ants are crawling around while the rubber band is stretching), but let's assume that clever physicists have found a way to correct for this. The scale factor is proportional to the distance between these two ants/galaxies.
I say "proportional" because it doesn't really matter what the distance is exactly; we just care about how that distance changes over time. Is the scale factor increasing as a constant rate? Or is it slowing down? Or is it accelerating? The answer ultimately depends on the theory of General Relativity, which is outside the scope of this post. There are, at least, some results of General Relativity which make intuitive sense (and others that do not make intuitive sense).
If the universe had no energy, we'd expect the scale factor to increase (or decrease) at a constant rate. "Inertia" is the intuitive explanation. As I explained in my previous post, a constant stretching rate implies that light from any galaxy will eventually reach us.
But since the universe has energy in it, that mass pulls itself together with gravity. So we'd expect the scale factor to slow down. But the rate at which the scale factor slows down depends on what kind of energy it is. If that energy comes from matter, the scale factor slows down at a certain rate. If that energy comes from massless particles like light, the scale factor slows down even at a greater rate.* The difference between matter and light is that they dilute at different rates as the universe stretches.
Now, if the energy comes from something that doesn't dilute at all, then the scale factor actually accelerates over time. I realize this is quite counterintuitive, but I'm postponing the explanation indefinitely until I understand it myself! In any case, that's what dark energy is. Dark energy is a transparent form of energy which doesn't get more dilute as the universe grows.
In summary,
Universe without energy: Scale factor increases at constant rate
Universe dominated by radiation: Scale factor slows down over time
Universe dominated by matter: Scale factor slows down (but not by quite as much)
Universe dominated by dark energy: Scale factor accelerates
Of course, the universe has a mix of the different kinds of energies. The early universe was dominated by radiation. But the radiation diluted away as the universe expanded, so the later universe was dominated by matter. But now the matter has diluted away, leaving a universe dominated by dark energy. So at first the scale factor slows down, but it eventually speeds up again.
You want more details, with graphs? There was this great paper called "Expanding Confusion: Common Misconceptions of Cosmological Horizons and the Superluminal Expansion of the Universe" with exactly that.
Here, I will introduce something called the scale factor. The scale factor is similar in concept to the total length of the rubber band. The tricky part is that there is no "total length" of the universe, because the universe (as far as we know) is infinitely long. But even if the rubber band were infinitely long, we can still imagine it stretching.
Even without referring to the "ends" of the rubber band, we can still see that the ants are getting further apart. Similarly, even though the universe has no "ends", we can still observe galaxies getting farther apart. There are some complications (like if the ants are crawling around while the rubber band is stretching), but let's assume that clever physicists have found a way to correct for this. The scale factor is proportional to the distance between these two ants/galaxies.
I say "proportional" because it doesn't really matter what the distance is exactly; we just care about how that distance changes over time. Is the scale factor increasing as a constant rate? Or is it slowing down? Or is it accelerating? The answer ultimately depends on the theory of General Relativity, which is outside the scope of this post. There are, at least, some results of General Relativity which make intuitive sense (and others that do not make intuitive sense).
If the universe had no energy, we'd expect the scale factor to increase (or decrease) at a constant rate. "Inertia" is the intuitive explanation. As I explained in my previous post, a constant stretching rate implies that light from any galaxy will eventually reach us.
But since the universe has energy in it, that mass pulls itself together with gravity. So we'd expect the scale factor to slow down. But the rate at which the scale factor slows down depends on what kind of energy it is. If that energy comes from matter, the scale factor slows down at a certain rate. If that energy comes from massless particles like light, the scale factor slows down even at a greater rate.* The difference between matter and light is that they dilute at different rates as the universe stretches.
Now, if the energy comes from something that doesn't dilute at all, then the scale factor actually accelerates over time. I realize this is quite counterintuitive, but I'm postponing the explanation indefinitely until I understand it myself! In any case, that's what dark energy is. Dark energy is a transparent form of energy which doesn't get more dilute as the universe grows.
In summary,
Universe without energy: Scale factor increases at constant rate
Universe dominated by radiation: Scale factor slows down over time
Universe dominated by matter: Scale factor slows down (but not by quite as much)
Universe dominated by dark energy: Scale factor accelerates
Of course, the universe has a mix of the different kinds of energies. The early universe was dominated by radiation. But the radiation diluted away as the universe expanded, so the later universe was dominated by matter. But now the matter has diluted away, leaving a universe dominated by dark energy. So at first the scale factor slows down, but it eventually speeds up again.
You want more details, with graphs? There was this great paper called "Expanding Confusion: Common Misconceptions of Cosmological Horizons and the Superluminal Expansion of the Universe" with exactly that.
Click to enlarge. This is based on the ΛCDM (Lambda Cold Dark Matter) model, assuming that the energy of the universe is currently 70% dark energy and 30% matter.
Some definitions to understand the graphs:
The comoving distance is simply the distance divided by the scale factor.
The dotted lines represent the paths of objects, provided they are not "crawling around", but just following the expansion of space.
The particle horizon is the answer to the question: how far can we see? Some 380,000 years after the big bang, the universe became transparent. (Update: the particle horizon is not defined from the point when the universe becomes transparent, but from the "beginning".) From that point on, light traveled from far away objects, and eventually it reached us. Simultaneously, those objects were getting further from us. The particle horizon refers to the current distance of those objects whose light from billions of years ago is just reaching us now. Currently, the particle horizon is 46 billion light years away. Therefore, the size of the observable universe is 93 billion light years across!
The hubble sphere is the distance at which the rate of expansion is equal to the speed of light. Beyond the hubble sphere, objects are receding from us faster than the speed of light. It's allowed to be faster than light, because it's an expansion of space, not motion through space. The relativistic speed limit only applies to the relative motion of objects that are near each other.
The light cone is the region of the universe's past that we can presently see. Remember that the further away we look, the further into the past we look. And the further back into the past, the more dense the universe used to be. This is not the same as the particle horizon, which refers to the current position of galaxies whose past we can see, not their past positions.
The event horizon is the largest region that will ever be in the light cone. If the scale factor were increasing at a constant rate (or decelerating), there would be no event horizon. That is, light from every part of the universe from any time would eventually reach us. But since the scale factor is accelerating, there is an event horizon. There are some parts of the universe that we will never see!
I hope this illuminates some of the many confusing aspects of cosmology. As the paper's title suggests, there are a variety of misconceptions about the expanding universe. One of those misconceptions is that the expansion of the universe isn't allowed to exceed the speed of light. This mistake is even made by physicists when speaking to the public! If you want to read more, I recommend a more popular version of this article, which appeared in Scientific American.
*These are based on solutions to the Friedmann equations in a flat universe.
The hubble sphere is the distance at which the rate of expansion is equal to the speed of light. Beyond the hubble sphere, objects are receding from us faster than the speed of light. It's allowed to be faster than light, because it's an expansion of space, not motion through space. The relativistic speed limit only applies to the relative motion of objects that are near each other.
The light cone is the region of the universe's past that we can presently see. Remember that the further away we look, the further into the past we look. And the further back into the past, the more dense the universe used to be. This is not the same as the particle horizon, which refers to the current position of galaxies whose past we can see, not their past positions.
The event horizon is the largest region that will ever be in the light cone. If the scale factor were increasing at a constant rate (or decelerating), there would be no event horizon. That is, light from every part of the universe from any time would eventually reach us. But since the scale factor is accelerating, there is an event horizon. There are some parts of the universe that we will never see!
I hope this illuminates some of the many confusing aspects of cosmology. As the paper's title suggests, there are a variety of misconceptions about the expanding universe. One of those misconceptions is that the expansion of the universe isn't allowed to exceed the speed of light. This mistake is even made by physicists when speaking to the public! If you want to read more, I recommend a more popular version of this article, which appeared in Scientific American.
*These are based on solutions to the Friedmann equations in a flat universe.
Wednesday, November 2, 2011
Dream: the little girl
I dreamt the story of a little girl with pigtails. Much of the details are lost, but the point was largely to show how bitter she was. Also, there is something wrong with her eyes. She's not blind, but her eyes look strangely dark, and no irises are visible.
I remember the end. The end comes in the form of a flashback. She's walking with a little black boy, her friend. She says bitterly to him, "You know, a black person once stole my eyes." The camera slowly shifts so that we see that at this younger age, her eyes still look mostly normal. She goes off, as the little boy stands there, somewhat angry. After a minute, the boy goes running after her, following her into a room where her mother is. Her mother is black. The boy shouts, "A black person didn't steal your eyes... you are black!" Suddenly, the audience understands... she is an albino black girl, and that's why she's so bitter.
Then my dream replays an earlier scene. There was one scene where it was said that the girl has to stay out of daylight at certain hours and undergo some light therapy. A white woman and man appear in this scene to help her, referring to themselves as "Your father and I". But in retrospect, it seems that they were really talking to a boy who was with her; they were the boy's parents.
The reveal seems like such a shameless and nonsensical retcon. For one thing, the girl obviously couldn't be albino since her hair was black (obviously based on Zimmy from Gunnerkrigg Court). One day I would like to write a work of fiction, but it's never gonna happen if my subconscious comes up with such terrible ideas.
I remember the end. The end comes in the form of a flashback. She's walking with a little black boy, her friend. She says bitterly to him, "You know, a black person once stole my eyes." The camera slowly shifts so that we see that at this younger age, her eyes still look mostly normal. She goes off, as the little boy stands there, somewhat angry. After a minute, the boy goes running after her, following her into a room where her mother is. Her mother is black. The boy shouts, "A black person didn't steal your eyes... you are black!" Suddenly, the audience understands... she is an albino black girl, and that's why she's so bitter.
Then my dream replays an earlier scene. There was one scene where it was said that the girl has to stay out of daylight at certain hours and undergo some light therapy. A white woman and man appear in this scene to help her, referring to themselves as "Your father and I". But in retrospect, it seems that they were really talking to a boy who was with her; they were the boy's parents.
The reveal seems like such a shameless and nonsensical retcon. For one thing, the girl obviously couldn't be albino since her hair was black (obviously based on Zimmy from Gunnerkrigg Court). One day I would like to write a work of fiction, but it's never gonna happen if my subconscious comes up with such terrible ideas.
Monday, October 31, 2011
Stumbling over their own rhetoric
I'm really late to this one, but PZ Myers had some posts criticizing Greg Epstein's humanist chaplaincy. If I read PZ correctly*, he doesn't like using a church-like model for community organization. If you want to read more, I recommend Crommunist's response (which inspired parts of this post).
*It is entirely possible that I misread him.
I think of this as atheists stumbling over their own rhetoric. Atheists openly criticize many aspects of religions, and for plenty of valid reasons too. But atheists, being human, will make mistakes about which aspects of religion cause it to be so bad.
For example: I've heard lots of atheists jokingly say that atheism is great because it frees up your Sundays. If these are the kind of idle jokes you make, you might have a negative reaction to atheist groups that have weekly meetings, particularly if they're on Sundays. But is that really what's wrong with Christianity, the mere fact that there is a tradition of Sunday meetings? Obviously not... But the rhetoric is there, and we're stumbling over it. And it sure doesn't help that outsiders will stupidly grab onto any similarity between atheists and religious people, as if that were a valid criticism of anything.
This may be a silly example. Who would let such an little thin get in the way of going to weekly meetings of atheists? Nobody I know, but then most of my vocal atheist friends I know through organizations that meet weekly.
I believe there is a whole collection of other examples of atheists stumbling over their own rhetoric.
Evangelism. We agree that evangelism is bad. What is bad about it? I consider it bad because it's done in socially awkward situations, and the views espoused are often offensive, wrong, and offensively wrong. But lots of atheists apparently think that trying to persuade people on religious topics is bad in general, and criticize other atheists as too evangelical.
Spirituality. Most atheists I know recognize that it is silly to let the lack of a spiritual realm get in the way of expressing awe, wonder, and other profound emotions. They do, however, see it as a good reason to not use the word "spirituality", since if spirits don't exist, that's not really what it is. I don't sympathize with the need for awe and wonder, but good for them for not letting any rhetoric prevent them from enjoying themselves!
Ritual. I quote PZ Myers: "Tapping into our psychology to get us to sit and get sucked into pointless ritual is not how I want to see the atheist movement evolve. I want us to think and act, not reassure ourselves by going through repetitive motions, through superstitious behavior." But then, I think lots of atheists are fans of Halloween, which is also filled with pointless rituals. (I don't particularly like Halloween.) What's that, some people enjoy Halloween? Who am I to begrudge that?
Priests. Obviously something has gone wrong with the Catholic priesthood, but what? Is it because any sort of leader or authority figure is bad? Is it because celibacy is unnatural? Surely we can think of a more nuanced reason that doesn't also apply to student group leaders, public intellectuals, or people who personally choose to remain celibate. How about... upholding a group as morally superior, to the point of concealing any evidence to the contrary?
Church. I must say that I completely agreed with PZ's title: "Atheist church? NO THANK YOU." I really hated church because it was boring. Also, I think church music is terrible. Yes, gospel music too. I think it is hypocritical that many atheists will say I'm letting my atheism get in the way of enjoying religious music (even though I also disliked it when I was religious), and simultaneously let their own atheism get in the way of recognizing the value of a church-like community structure. Are we incapable of seeing that different people have different tastes?
I certainly don't share the taste of atheists who feel the need for a humanist chaplaincy, but I don't see what is so wrong with that. People can do what they want, or not do what they don't want. People can also complain about other people's terrible taste. But let's not get completely carried away there.
*It is entirely possible that I misread him.
I think of this as atheists stumbling over their own rhetoric. Atheists openly criticize many aspects of religions, and for plenty of valid reasons too. But atheists, being human, will make mistakes about which aspects of religion cause it to be so bad.
For example: I've heard lots of atheists jokingly say that atheism is great because it frees up your Sundays. If these are the kind of idle jokes you make, you might have a negative reaction to atheist groups that have weekly meetings, particularly if they're on Sundays. But is that really what's wrong with Christianity, the mere fact that there is a tradition of Sunday meetings? Obviously not... But the rhetoric is there, and we're stumbling over it. And it sure doesn't help that outsiders will stupidly grab onto any similarity between atheists and religious people, as if that were a valid criticism of anything.
This may be a silly example. Who would let such an little thin get in the way of going to weekly meetings of atheists? Nobody I know, but then most of my vocal atheist friends I know through organizations that meet weekly.
I believe there is a whole collection of other examples of atheists stumbling over their own rhetoric.
Evangelism. We agree that evangelism is bad. What is bad about it? I consider it bad because it's done in socially awkward situations, and the views espoused are often offensive, wrong, and offensively wrong. But lots of atheists apparently think that trying to persuade people on religious topics is bad in general, and criticize other atheists as too evangelical.
Spirituality. Most atheists I know recognize that it is silly to let the lack of a spiritual realm get in the way of expressing awe, wonder, and other profound emotions. They do, however, see it as a good reason to not use the word "spirituality", since if spirits don't exist, that's not really what it is. I don't sympathize with the need for awe and wonder, but good for them for not letting any rhetoric prevent them from enjoying themselves!
Ritual. I quote PZ Myers: "Tapping into our psychology to get us to sit and get sucked into pointless ritual is not how I want to see the atheist movement evolve. I want us to think and act, not reassure ourselves by going through repetitive motions, through superstitious behavior." But then, I think lots of atheists are fans of Halloween, which is also filled with pointless rituals. (I don't particularly like Halloween.) What's that, some people enjoy Halloween? Who am I to begrudge that?
Priests. Obviously something has gone wrong with the Catholic priesthood, but what? Is it because any sort of leader or authority figure is bad? Is it because celibacy is unnatural? Surely we can think of a more nuanced reason that doesn't also apply to student group leaders, public intellectuals, or people who personally choose to remain celibate. How about... upholding a group as morally superior, to the point of concealing any evidence to the contrary?
Church. I must say that I completely agreed with PZ's title: "Atheist church? NO THANK YOU." I really hated church because it was boring. Also, I think church music is terrible. Yes, gospel music too. I think it is hypocritical that many atheists will say I'm letting my atheism get in the way of enjoying religious music (even though I also disliked it when I was religious), and simultaneously let their own atheism get in the way of recognizing the value of a church-like community structure. Are we incapable of seeing that different people have different tastes?
I certainly don't share the taste of atheists who feel the need for a humanist chaplaincy, but I don't see what is so wrong with that. People can do what they want, or not do what they don't want. People can also complain about other people's terrible taste. But let's not get completely carried away there.
Wednesday, October 26, 2011
An answer to a nosy question
If you're asexual, do you masturbate?
This is, in my experience, the most frequently asked question about asexuality (although usually people use a euphemism). Here is my straight answer:
Presumably you are not so much interested in my personal life, but interested in whether asexual people in general masturbate. Unfortunately, answering the question directly would not satisfy your curiosity, because A) you don't know whether I am representative of asexuals, and B) you probably don't have any idea how much non-asexual people masturbate either.
What you really want is some capital-letter SCIENCE!
No, really. In general, it is very difficult to scientifically quantify asexuality, but it's relatively easy to just make a survey asking how often people masturbate. Someone must have done it.
I'll save you time. A survey was hidden in this paper by Prause and Graham.
But how can that be?
Forget how things can be the way they are. They just are. We've shown it empirically with SCIENCE!
But presumably you meant to ask, how is this consistent with the definition of asexuality? An asexual plus sexuality equals not-an-asexual, am I right?
No, that's the wrong definition of asexuality. Asexuality does not mean a lack of sexuality, it means a lack of sexual attraction (or sexual interest or sexual desire--the definitions vary). In other words, there are multiple dimensions of sexuality, and asexuality just refers to one of those dimensions. One of the reasons asexuality is so hard to study is because suddenly it becomes necessary to disentangle all these different dimensions that people usually assume go together. Masturbation and sexual attraction are two of the easiest dimensions to disentangle; even a survey can do it.
Other frequent questions: Do asexuals think of it as a sexual activity? What do asexuals masturbate to?
Unfortunately I don't think this is in the scientific literature (you may scan it for yourself). Based on the accounts I've seen, nearly all answers are possible. Asexuals may think of it as sexual, or not. They may masturbate to objects, concepts, people, or nothing in particular. If that seems strange... I am not really sure what is meant by a non-strange sexuality. Anyways, it is hard to tell whether this is statistically different or similar to non-asexual masturbation habits.
Another frequent question: Is it strange or creepy of me to ask about this?
Not strange, no. It is creepy though. It was probably also creepy of me to answer.
This is, in my experience, the most frequently asked question about asexuality (although usually people use a euphemism). Here is my straight answer:
Presumably you are not so much interested in my personal life, but interested in whether asexual people in general masturbate. Unfortunately, answering the question directly would not satisfy your curiosity, because A) you don't know whether I am representative of asexuals, and B) you probably don't have any idea how much non-asexual people masturbate either.
What you really want is some capital-letter SCIENCE!
No, really. In general, it is very difficult to scientifically quantify asexuality, but it's relatively easy to just make a survey asking how often people masturbate. Someone must have done it.
I'll save you time. A survey was hidden in this paper by Prause and Graham.
(From Table 2) Frequency of masturbation:The followup question that everyone asks is...
asexuals: 3.7 +/- 2
non-asexuals: 4.5 +/- 1.9
The scale is from 1 (never masturbated) to 7 (4 times/week or more)
But how can that be?
Forget how things can be the way they are. They just are. We've shown it empirically with SCIENCE!
But presumably you meant to ask, how is this consistent with the definition of asexuality? An asexual plus sexuality equals not-an-asexual, am I right?
No, that's the wrong definition of asexuality. Asexuality does not mean a lack of sexuality, it means a lack of sexual attraction (or sexual interest or sexual desire--the definitions vary). In other words, there are multiple dimensions of sexuality, and asexuality just refers to one of those dimensions. One of the reasons asexuality is so hard to study is because suddenly it becomes necessary to disentangle all these different dimensions that people usually assume go together. Masturbation and sexual attraction are two of the easiest dimensions to disentangle; even a survey can do it.
Other frequent questions: Do asexuals think of it as a sexual activity? What do asexuals masturbate to?
Unfortunately I don't think this is in the scientific literature (you may scan it for yourself). Based on the accounts I've seen, nearly all answers are possible. Asexuals may think of it as sexual, or not. They may masturbate to objects, concepts, people, or nothing in particular. If that seems strange... I am not really sure what is meant by a non-strange sexuality. Anyways, it is hard to tell whether this is statistically different or similar to non-asexual masturbation habits.
Another frequent question: Is it strange or creepy of me to ask about this?
Not strange, no. It is creepy though. It was probably also creepy of me to answer.
Monday, October 24, 2011
The ant and the universe
Because light in our universe has had a finite amount of time to travel, we can only see a finite part of our universe. We call this the observable universe. But did you know that, even though the age of the universe is 13.7 billion years, we can actually see further than 13.7 billion light-years?
According to Hubble's Law, distant galaxies are receding from us at a speed proportional to their distance. In fact, beyond 13.8 billion light years away, objects are receding from us faster than light. Did you know that the furthest objects we see are actually receding faster than light?
Believe it or not, these facts are easy to understand with only elementary knowledge of cosmology.
There is a classic puzzle involving an ant on a rubber band. The ant tries to run from one end of the rubber band to the other, but every second we stretch the rubber band longer. Will the ant ever reach the other side, or will it just get further and further from its destination as the rubber band stretches?
The ant on the rubber band is a lot like the path of light through the expanding universe. The ant crawls at a constant speed, but only relative to the rubber band. As the rubber band stretches, the ant may become further from its destination. Similarly, light travels at a constant speed. But as space itself expands, light from far away galaxies may actually become further from us over time.
(Note that the far away galaxies aren't breaking any speed limit even if they recede faster than light. They are receding because the space between us is expanding. The relativistic speed limit only applies to the relative velocities of two objects at nearly the same location. Analogously, we can say that even if we stretch the rubber band really fast, this doesn't mean the ant is breaking its own crawling-speed limit. It just means the rubber band is stretching.)
So, will the ant make it or not? It depends how quickly we stretch the rubber band. If we were feeling devious, we could stretch the rubber band at exactly the right rate so that the ant is running in place, never getting any closer to its destination. But let's consider a stretching rate which is a little more like our universe. Suppose that the ant crawls one inch per second, and each second we stretch the total rubber band's length by one foot.
At first, the ant will gain an inch, and lose a foot. But after the ant covers some distance, I waste a lot of effort stretching the part of the rubber band that is already behind the ant. So eventually, the ant may catch up! Indeed, we can show that it will catch up, if we consider the total fraction of rubber band that the ant covers each second. In the first second, the ant covers 1/12 of the rubber band. In the second second, it covers 1/12 * 1/2 of the rubber band (since now the rubber band has been stretched to twice its previous length.) The next second, the ant covers 1/12 * 1/3. And so forth. We get a sequence like this:
The series in parentheses is known as the harmonic series. The harmonic series can arbitrarily big, just by adding more terms (but it takes an exponentially large number of terms). If we were to graph the ant's trajectory, it would look like this:
So that's how the ant traverses the rubber band even though the rubber band was stretching faster than the ant could crawl. Similarly, light can reach us from far away galaxies even if they're receding faster than light.
How far did the ant travel? The ant is traveling an inch per second, and traveled for over 160,000 seconds. Therefore, it traveled over 160,000 inches. But there's another distance we can ask about: How far away is the point on the rubber band from which the ant started? Because the opposite end of the rubber band moves at a foot per second, it must be over 160,000 feet away.
With light we can ask the same questions. According to NASA, the furthest galaxy we know of is 13.2 billion light years away, by which they really mean that the light has traveled 13.2 billion light years to get to us. But how far away is that galaxy now? It is probably much further than 13.7 billion light years away, because it is receding from us very quickly.
But there are additional complications when we apply this to the universe. As it turns out, the universe does not expand at a uniform rate, like our rubber band. The two additional complications are matter and dark energy. This will be explained in the next part.
According to Hubble's Law, distant galaxies are receding from us at a speed proportional to their distance. In fact, beyond 13.8 billion light years away, objects are receding from us faster than light. Did you know that the furthest objects we see are actually receding faster than light?
Believe it or not, these facts are easy to understand with only elementary knowledge of cosmology.
There is a classic puzzle involving an ant on a rubber band. The ant tries to run from one end of the rubber band to the other, but every second we stretch the rubber band longer. Will the ant ever reach the other side, or will it just get further and further from its destination as the rubber band stretches?
An ant comes across a rubber band... (Ant image from here)
The ant on the rubber band is a lot like the path of light through the expanding universe. The ant crawls at a constant speed, but only relative to the rubber band. As the rubber band stretches, the ant may become further from its destination. Similarly, light travels at a constant speed. But as space itself expands, light from far away galaxies may actually become further from us over time.
(Note that the far away galaxies aren't breaking any speed limit even if they recede faster than light. They are receding because the space between us is expanding. The relativistic speed limit only applies to the relative velocities of two objects at nearly the same location. Analogously, we can say that even if we stretch the rubber band really fast, this doesn't mean the ant is breaking its own crawling-speed limit. It just means the rubber band is stretching.)
So, will the ant make it or not? It depends how quickly we stretch the rubber band. If we were feeling devious, we could stretch the rubber band at exactly the right rate so that the ant is running in place, never getting any closer to its destination. But let's consider a stretching rate which is a little more like our universe. Suppose that the ant crawls one inch per second, and each second we stretch the total rubber band's length by one foot.
At first, the ant will gain an inch, and lose a foot. But after the ant covers some distance, I waste a lot of effort stretching the part of the rubber band that is already behind the ant. So eventually, the ant may catch up! Indeed, we can show that it will catch up, if we consider the total fraction of rubber band that the ant covers each second. In the first second, the ant covers 1/12 of the rubber band. In the second second, it covers 1/12 * 1/2 of the rubber band (since now the rubber band has been stretched to twice its previous length.) The next second, the ant covers 1/12 * 1/3. And so forth. We get a sequence like this:
The series in parentheses is known as the harmonic series. The harmonic series can arbitrarily big, just by adding more terms (but it takes an exponentially large number of terms). If we were to graph the ant's trajectory, it would look like this:
Note: I calculated this assuming continuous stretching, not by discrete stretching. This is more true to cosmology.
So that's how the ant traverses the rubber band even though the rubber band was stretching faster than the ant could crawl. Similarly, light can reach us from far away galaxies even if they're receding faster than light.
How far did the ant travel? The ant is traveling an inch per second, and traveled for over 160,000 seconds. Therefore, it traveled over 160,000 inches. But there's another distance we can ask about: How far away is the point on the rubber band from which the ant started? Because the opposite end of the rubber band moves at a foot per second, it must be over 160,000 feet away.
With light we can ask the same questions. According to NASA, the furthest galaxy we know of is 13.2 billion light years away, by which they really mean that the light has traveled 13.2 billion light years to get to us. But how far away is that galaxy now? It is probably much further than 13.7 billion light years away, because it is receding from us very quickly.
But there are additional complications when we apply this to the universe. As it turns out, the universe does not expand at a uniform rate, like our rubber band. The two additional complications are matter and dark energy. This will be explained in the next part.
Friday, October 21, 2011
Old news: Today is the end
Here's an old story from May 24th:
I'd be sort of interested if the same prediction was made by the quake quack. That would be like alignment of the planets, but instead of planets, different spheres of woo. Alas! A glance suggests that there is no such alignment.
Harold Camping, who announced the Rapture would occur Saturday [May 21], has had another revelation: The world will now end on October 21.Harold Camping claims the world will end by earthquake. I'm not sure what exact hour. Actually here we had a couple of quakes yesterday!
I'd be sort of interested if the same prediction was made by the quake quack. That would be like alignment of the planets, but instead of planets, different spheres of woo. Alas! A glance suggests that there is no such alignment.
Wednesday, October 19, 2011
The ant and the rubber band
In a draft I'm writing, I'm including a classic puzzle as a demonstrative example. But I should let my readers have a try first!
There is an ant on a rubber band. The ant is crawling from one end of the rubber band towards the other at 1 inch per second. The rubber band is one foot long, but getting longer. After each second, the rubber band's length grows by one foot.
Question: Will the ant ever reach the other side of the rubber band?
(It's an infinitely stretchy rubber band, and the ant lives infinitely long. Since I am a physicist, I will not worry about whether the rubber band is stretching instantaneously every second or stretching continuously. Just assume whichever you prefer.)
You have less than a week to solve this one. Bonus points if you can predict what my draft is about.
(solution contained here)
There is an ant on a rubber band. The ant is crawling from one end of the rubber band towards the other at 1 inch per second. The rubber band is one foot long, but getting longer. After each second, the rubber band's length grows by one foot.
Question: Will the ant ever reach the other side of the rubber band?
(It's an infinitely stretchy rubber band, and the ant lives infinitely long. Since I am a physicist, I will not worry about whether the rubber band is stretching instantaneously every second or stretching continuously. Just assume whichever you prefer.)
You have less than a week to solve this one. Bonus points if you can predict what my draft is about.
(solution contained here)
Tuesday, October 18, 2011
Woohoo, 4th bloggiversary!
This year, I remembered my mother's birthday, but not my blog's (which was on October 5th). Ah well, my blog probably doesn't care as much as my mother would.
So, another year, another set of highlights:
Physics!
Dreaming boltzmann brains
Electricity, magnetism, space, and time
One: the universe's favorite digit
Atheism!
The interminable tone debate
Religion-shaped hole: spirituality
Critical thinking!
Nature/Nurture and causality
Astrology: a different nonsense than you thought
Opinions are relative
Asexuality!
A brief history of antisexuality
Erasure: What's the harm?
On asexual relationships
Puzzles!
Fractal maze
The tiger and the lake
Miscellaneous!
Actual and potential infinities (a new series spanning math, physics, and the cosmological argument)
(Also see last bloggiversary's link roundup)
Looking back, I think the hardest posts to pick are the physics ones. I really like most of my physics posts, and many of my thoughts on critical thinking seem too rambly and poorly formed in retrospect. It probably has to do with the fact that physics posts require more effort, giving me more time to think about the way they're framed. But another possible explanation is that physics is easy, critical thinking is hard.
So, another year, another set of highlights:
Physics!
Dreaming boltzmann brains
Electricity, magnetism, space, and time
One: the universe's favorite digit
Atheism!
The interminable tone debate
Religion-shaped hole: spirituality
Critical thinking!
Nature/Nurture and causality
Astrology: a different nonsense than you thought
Opinions are relative
Asexuality!
A brief history of antisexuality
Erasure: What's the harm?
On asexual relationships
Puzzles!
Fractal maze
The tiger and the lake
Miscellaneous!
Actual and potential infinities (a new series spanning math, physics, and the cosmological argument)
(Also see last bloggiversary's link roundup)
Looking back, I think the hardest posts to pick are the physics ones. I really like most of my physics posts, and many of my thoughts on critical thinking seem too rambly and poorly formed in retrospect. It probably has to do with the fact that physics posts require more effort, giving me more time to think about the way they're framed. But another possible explanation is that physics is easy, critical thinking is hard.
Monday, October 17, 2011
A lot of Brillouin Zones
In condensed matter physics we deal a lot with crystals, which is a repeating structure of atoms. Every crystal is associated with a lattice,* which is an infinitely repeating set of points.
For example, if the points shown above were to repeat infinitely over the plane, they would make a lattice.
A useful concept is the first Brillouin Zone, which is the set of all points which are closer to the center point of the lattice than to any other point of the lattice. In the above example, the first Brillouin Zone would simply be a square around the center.
Interestingly (but less usefully) there is also a definition for the Nth Brillouin Zone. The Nth Brillouin Zone is the set of all points such that the center point of the lattice is the Nth closest point in the lattice. I thought it might be pretty to draw the first few Brillouin Zones, and then I went totally overboard.
The Brillouin Zones have the interesting property that each one has equal area. And for any given Brillouin Zone, you can translate the different pieces by integer distances and form a square out of them.
I think one thing that attracted me to condensed matter physics is that there's all this geometry in it... and it's actually useful for describing reality. Not this Nth Brillouin Zone stuff though, that's useless. Hardly anyone thinks about the second Brillouin Zone, much less the third or twenty-seventh.
You can get Brillouin Zones of different shapes if you have different kinds of lattices! And you can even have 3D lattices, producing 3D Brillouin Zones. Note that even though real crystals exist in 3-dimensional space, they can be layered in 2D structures and thus be associated with 2D lattices. For example, the 2D lattice I showed is the correct lattice to use for the cuprate superconductors that I study.
*The locations of the atomic nuclei in a crystal often make a lattice, but for complicated reasons, this is not the one I'm talking about. Every crystal is also associated with a completely different "reciprocal lattice", which is the one relevant to Brillouin Zones.
For example, if the points shown above were to repeat infinitely over the plane, they would make a lattice.
A useful concept is the first Brillouin Zone, which is the set of all points which are closer to the center point of the lattice than to any other point of the lattice. In the above example, the first Brillouin Zone would simply be a square around the center.
Interestingly (but less usefully) there is also a definition for the Nth Brillouin Zone. The Nth Brillouin Zone is the set of all points such that the center point of the lattice is the Nth closest point in the lattice. I thought it might be pretty to draw the first few Brillouin Zones, and then I went totally overboard.
The first 27 Brillouin Zones. The first Brillouin Zone is the red square in the center, and successive Brillouin Zones are each in a different color, moving outwards. Click to enlarge.
The Brillouin Zones have the interesting property that each one has equal area. And for any given Brillouin Zone, you can translate the different pieces by integer distances and form a square out of them.
I think one thing that attracted me to condensed matter physics is that there's all this geometry in it... and it's actually useful for describing reality. Not this Nth Brillouin Zone stuff though, that's useless. Hardly anyone thinks about the second Brillouin Zone, much less the third or twenty-seventh.
You can get Brillouin Zones of different shapes if you have different kinds of lattices! And you can even have 3D lattices, producing 3D Brillouin Zones. Note that even though real crystals exist in 3-dimensional space, they can be layered in 2D structures and thus be associated with 2D lattices. For example, the 2D lattice I showed is the correct lattice to use for the cuprate superconductors that I study.
*The locations of the atomic nuclei in a crystal often make a lattice, but for complicated reasons, this is not the one I'm talking about. Every crystal is also associated with a completely different "reciprocal lattice", which is the one relevant to Brillouin Zones.
Subscribe to:
Posts (Atom)